Consensus Analysis

Steve Borgatti, Boston College

Consensus analysis is both a theory and a method. As a theory, it specifies the conditions under which more agreement among individuals on the right answers to a "test" indicates more knowledge on their part. As a method, it provides a way to uncover the culturally correct answers to a set of questions in the face of certain kinds of intra-cultural variability. At the same time, it enables the researcher to assess the extent of knowledge possessed by an informant about a given cultural domain.

Consider a multiple choice exam given an introductory anthropology class. A possible question might be "The author of Tristes Tropiques was _______", followed by 5 choices. If we treat the students' responses as data we obtain a rectangular, respondent-by-question matrix X in which x_ij gives student i's choice on the jth question. Each row of the matrix is a vector of numbers, ranging from 1 to 5, representing a given student's responses to each question. The answer key is also a vector, with the same range of values, representing the instructor's responses. To obtain each student's score, we compare the student's vector with the instructor's vector. If the two vectors are the same across all questions, the student gets a perfect score. If the vectors are quite different, the student has missed many questions and gets a low score. The important point is that a student's score on the exam is actually a measure of similarity between the student's and instructor's vectors. The measure of similarity is the simple match coefficient: it is the number of times (questions) that the student and the instructor got the same answer, divided by the number of questions.

Of course, we can compute the similarity between any two vectors, not just a student's with an instructor's. Let's consider the similarity between two students' vectors. If both students got perfect scores on the exam, then their vectors will be identical, assuming there is only one right answer to each question. If both students did pretty well, then again we expect a certain amount similarity in their pattern of answers, because on all questions that they both got right, they will have the same answer. On questions that one got right and the other got wrong, they will definitely have different answers. And on questions which both got wrong, they will usually have different answers, because for each question there are several wrong answers to choose from. The more questions they get wrong, the less the similarity we expect between their response vectors. If two students each got very few questions right, the similarity between their response vectors (assuming no cheating or other bias), should be no better than chance level.

This thought experiment suggests, that agreement between students (i.e. similarity of response vectors) is a function of each student's knowledge of the subject matter, at least under ideal conditions. Let us specify more clearly what these conditions are. Implicitly, we have assumed a test situation in which there is one and only one right answer to each question. We also assume a student response model of the following sort:

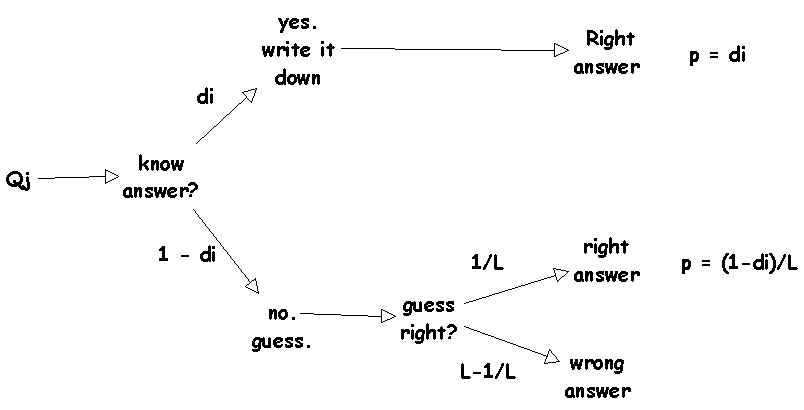
If the student knows the answer to a question, she writes it down without error (i.e., gets it right) and moves on to the next question. If the student doesn't know the answer, she guesses randomly among all the choices. Let's use d_i to denote the probability that the ith student knows the right answer to any given question. We can think of d_i as the proportion of all possible questions about a given topic that student i knows the answer to.

The probability that i doesn't know the answer is 1-d_i. Given that she doesn't the answer to a given question, the probability that she will get the question right by guessing is 1/L, where L is the number of alternatives (in this case, 5). We are of course assuming that she is not predisposed to always pick, say, the middle answer, and that she cannot eliminate absurd alternatives. If she can eliminate some alternatives, the probability of guessing right is given by 1/L^*, where L^* is the number of choices left. In any case, the probability of getting a given question right is the probability of knowing the right answer, plus the probability of guessing right.

We can see that the total probability of getting a question right is

m_i = d_i + (1 - d_i)/L = prob of getting Qj right

and the probability of knowing the answer ("competence" is

d_i = (Lm_i - 1)/(L-1) = prob of knowing answer

Using this simple model, we can retrace our thought experiment to get a more precise statement about the relationship between agreement and knowledge. We begin by formulating the probability that two students i and j, with knowledge levels d_i and d_j respectively, give the same answer to a given question. There are four ways it can happen:

1. Both i and j know the right answer.

p(both know) = d_id_j

2. Student i knows the right answer, and student j guesses right.

p(i knows, j guesses) = d_i(1-d_j)/L

3. Student j knows the right answer, and student i guesses right.

p(j knows, i guesses) = d_j(1-d_i)/L

4. Neither knows the right answer, but both guess the same answer (regardless of whether its right or wrong).

p(neither knows, guess the same) = (1-d_i)(1-d_j)/L

The probability that i and j give the same answer to any given question is denoted by m_ij and is simply the sum of the four probabilities above, as follows:

m_ij = d_id_j + d_i(1-d_j)/L + d_j(1-d_i)/L + (1-d_i)(1-d_j)/L
m_ij = d_id_j + (1 - d_id_j) /L

Thus, the agreement between i and j is given by the product of their respective competencies. This is the key theoretical result: given a test situtation and student response model as outlined above, it is incontrovertible that agreement implies knowledge and vice versa. The assumptions of this model can be summarized as follows:

1. Common Truth. There is one and only one right answer for every question. This is implied by the first fork in the response model where if the student knows the answer, they write it down.

2. Local Independence. Students' responses are independent (across students and questions), conditional on the truth. This is implied in the second fork of the response model, where if a student does not know the answer, she guesses randomly among the available choices.

3. Item Homogeneity. Questions are drawn randomly from a universe of possible questions, so that the probability d_i that student i knows the answer to a question is the same for all questions. Thus, all questions are on the same topic, about which a given student has a fixed level of knowledge. This is implied in the response model by the use of a single parameter d_i to characterize a respondent's probability of knowing the answer.

We now turn to the key practical result. In the last equation, m_ij (the proportion of questions that students i and j answered the same) is known. We can look at two student response vectors, and compute the proportion of matches. And in a test situation, where we have an answer key, we can also compute the d parameters, since they are just the percentage of questions answered correctly, minus a correction for chance guessing. But suppose we do not have the answer key. The equation can be rewritten as follows:

d_id_j = (Lm_ij - 1)/(L-1) = m^*_ij

This says that the products of the unknown parameters d are equal to observed similarities between students' responses, corrected for guessing. The observed similarities are the m_ijs. After correcting for chance, we get m^*_ij, which is just a rescaling of the observed similarities. This new equation can be solved via minimum residual factor analysis (Comrey) to yield least squares estimates of the d parameters.

In other words, even if we have lost the answer key, we can still find out exactly how much knowledge each student has by factor analyzing the pattern of student-student similarities. And given that we can tell who knows what they're doing and who doesn't, we can also determine what the right answers must have been to each question. That is, we can determine what the most probable answer was to any given question, given knowledge of who gave what answer. For example, if all 20 students who got more than 90% of the questions right said that the answer to question 7 was "b", the likelihood that it is not "b" is extremely remote, regardless of what the majority of students might have said.

This result is of tremendous significance for cultural anthropologists, who typically do not know the answers to the questions they are asking (!). One of the problems faced by anthropologists is the existence of cultural variability. If we ask basic questions of a sample of informants, even in matters of presumed "fact", we receive a variety of conflicting answers. We are not talking here of matters of personal preference, such as what do you like to do in your spare time, but more general questions which all respondents may agree have a single "right" answer -- yet disagree on what it is. Sometimes such disagreement is due to subcultural variability: there are in effect as many truths as subcultures. Yet even within a subculture, there may be differences in knowledge (or "cultural literacy" to put it in contemporary terms) which result in different answers. For example, I am not very good at identifying neighborhood trees or plants. An anthropologist asking me for the names of plants is likely to get many wrong answers. On the other hand, I have a good memory for names and dates of European historical interest. The methodology of consensus analysis permits the anthropologist to (a) discover the right answers and (b) determine who knows about a given topic and who doesn't.

It is important to note that, in this context, the "right answer" to a question is a culturally defined concept. We are not talking about truth in the Western folk-scientific sense of empirical reality. To name a tree correctly I do not conduct a biological investigation: I access the culture that assigns it a name. Knowing the right answer to "is the earth flat?" has nothing to do with understanding astronomy or geology: it is a function of one's access to the culture of a given group.

The methodology of consensus analysis depends on the three assumptions outlined earlier. Translated into the anthropological context, they are as follows:

1. One Culture. It is assumed that, whatever cultural reality might be, it is the same for everyone. There are no subcultures that have systematically different views on a given topic. All variability is due to variations in amount of knowledge.

2. Independence. The only force drawing people to a given answer is the culturally correct answer. When informants do not know an answer, they choose or make up one independently of each other. In other words, interview each respondent individually rather than in groups, and try to prevent the respondent from getting into a "response set", such as always answering "yes".

3. One Domain. All questions are drawn from the same underlying domain: you must not mix questions about tennis with questions about plants, because a person's knowledge of tennis may be very different from their knowledge of plants.

If these assumptions hold, you can rely on the estimates of the degree of knowledge an informant has, and what the right answers are. In addition, the ANTHROPAC implementation of consensus analysis can help test whether the assumptions hold, or more precisely, they can test whether the assumptions do not hold. One such test is the computation of the eigenvalues of the M^* matrix. The One Culture assumption is inconsistent with the existence of more than one large eigenvalue. Two large eigenvalues, for instance, is strong evidence that (at least) two truths (two systematically different patterns of responses) are governing the responses of informants. The program prints the ratio of the first eigenvalue to the second. The rule of thumb is that if the ratio is less than 3 to 1, the assumption of One Culture is indefensible. A ratio of 10 to 1 provides strong support, but can never prove, that the assumption is valid.