
Pilesorts
The pilesort task is used primarily to elicit from respondents judgements of similarity among items in a cultural domain. It can also be used to elicit the attributes that people use to distinguish among the items. There are many variants of the pilesort sort technique. We begin with the free pilesort.
Collecting Pilesort Data
The typical free pilesort technique begins with a set of 3-by-5 cards on which the name or short description of a domain item is written. For example, for the cultural domain of illnesses, we might have a set of 80 cards, one for each illness. For convenience, a unique ID number is written on the back of each card. The stack of cards is shuffled randomly and given to a respondent with the following instructions: "Here are a set of cards representing kinds of illnesses. I'd like you to sort them into piles according to how similar they are. You can make as many or as few piles as you like. Go!"
In some cases, it is better to do it in two steps. First you ask the respondent to look at each card to see if they recognize the illness. Ask them to set aside any cards representing illness terms that they are unfamiliar with. Then, with the remaining cards, have them do the sorting exercise.
Sometimes, respondents object to having to put a given item into just one pile. They feel that the item fits equally well into two different piles. This is perfectly acceptable. In such cases, I simply take a blank card, write the name of the item on the card, and let them put one card in each pile. As discussed in a later section, putting items into more than one pile causes no problems for analyzing the data, and may correspond better to the respondents' views. The only problem it creates is that it makes it more difficult later on to check whether the data were input correctly, since having an item appear in more than one pile is usually a sign that someone has mistyped an ID code.
Instead of writing names of items on cards, it is sometimes possible to sort pictures of the items, or even the items themselves (e.g., when working with the folk domain of "bugs"). However, it is my belief that, for literate respondents, the written method is always best. Showing pictures or using the items themselves tends to bias the respondents toward sorting according to physical attributes such as size, color and shape. For example, sorting pictures of fish yields sorts based on body shape and types of fins (Boster and Johnson, 1989). In contrast, sorting names of fish allows hidden attributes to affect the sorting (such as taste, where the fish is found, what it is used for, how it is caught, what it eats, how it behaves, etc.).
Normally, the pilesort exercise is repeated with at least 30 respondents(6), although the number depends on the amount of variability in responses. For example, if everyone in a society would give exactly the same answers, you would only need one respondent. But if there is a great deal of variability, you may need hundreds of sorts to get a good picture of the modal answers (i.e., the most common responses), and so that you can cut the data into demographic subgroups so that you can see how different groups sort things differently.
Analyzing Pilesort Data
The data are then tabulated and interpreted as follows. Every time a respondent places a given pair of items in the same pile together, we count that as a vote for the similarity of those two items (see Table 4). In the domain of animals, if all of the respondents place "coyote" and "wolf" in the same pile, we take that as evidence that these are highly similar items. In contrast, if no respondents put "salamander" and "moose" in the same pile, we understand that to mean that salamanders and moose are not very similar. We further assume that if an intermediate number of respondents put a pair of items in the same pile this means that the pair are of intermediate similarity.
Table 4. Percent of
Respondents Placing Each Pair of Items
in the Same Pile.
| Frog | Salam. | Beaver | Raccoon | Rabbit | Mouse | Coyote | Deer | Moose | |
| Frog | 100 | 96 | 6 | 2 | 2 | 0 | 0 | 2 | 2 |
| Salamander | 96 | 100 | 4 | 0 | 0 | 2 | 0 | 0 | 0 |
| Beaver | 6 | 4 | 100 | 62 | 65 | 56 | 17 | 25 | 13 |
| Raccoon | 2 | 0 | 62 | 100 | 71 | 58 | 23 | 29 | 15 |
| Rabbit | 2 | 0 | 65 | 71 | 100 | 75 | 17 | 27 | 15 |
| Mouse | 0 | 2 | 56 | 58 | 75 | 100 | 17 | 15 | 10 |
| Coyote | 0 | 0 | 17 | 23 | 17 | 17 | 100 | 21 | 15 |
| Deer | 2 | 0 | 25 | 29 | 27 | 15 | 21 | 100 | 77 |
| Moose | 2 | 0 | 13 | 15 | 15 | 10 | 15 | 77 | 100 |
*Data collected by Sandy Anderson under the direction of John Gatewood.
This interpretation of agreement as monotonically(7) related to similarity is not trivial and is not widely understood. It reflects the adoption of a set of simple process models for how respondents go about solving the pilesort task. One such model is as follows. Each respondent has the equivalent of a similarity metric in her head (e.g., she has a spatial map of the items in semantic space). However, the pilesort task essentially asks her to state, for each pair of items, whether the items are similar or not. Therefore, she must convert a continuous measure of similarity or distance into a yes/no judgement. If the similarity of the two items is very high, she places, with high probability, both items in the same pile. If the similarity is very low, she places the items, with high probability again, in different piles. If the similarity is intermediate, she essentially flips a coin (i.e., the probability of placing in the same pile is near 0.5). This process is repeated across all the respondents, leading the highly similar items to be placed in the same pile most of the time, and the dissimilar items to be placed in different piles most of the time. The items of intermediate similarity are placed together by approximately half the respondents, and placed in separate piles by the other half, resulting in intermediate similarity scores.
An alternative model, not inconsistent with the first one, is that people think of items as bundles of features or attributes. When asked to place items in piles, they place the ones that have mostly the same attributes in the same piles, and place items with mostly different attributes in separate piles. Items that share some attributes and not others have intermediate probabilities of being placed together, and this results in intermediate proportions of respondents placing them in the same pile.
Both these models are quite plausible. However, even if either or both is true, there is still a problem with the interpretation of intermediate percentages of respondents placing a pair of items in the same pile. Just because intermediate similarity implies intermediate consensus does not mean that the converse is true, namely that intermediate consensus implies intermediate similarity. For example, suppose half the respondents clearly understand that shark and dolphin are very similar (because they are large ocean predators) and place them in the same pile, while the other half are just as clear on the idea that shark and dolphin are quite dissimilar (because one is a fish and the other is a mammal). The result would be 50% of respondents placing shark and dolphin in the same pile, but we would NOT want to interpret this as meaning that 100% of respondents saw shark and dolphin as moderately similar. In other words, the measurement of similarity via aggregating pilesorts depends crucially on the assumption of underlying cultural consensus (Romney, Weller and Batchelder, 1986). There cannot be different systems of classification among the respondents or else we cannot interpret the results.
To some extent, this same problem afflicts the interpretation of freelist data as well. Items that are mentioned by a moderate or small proportion of respondents are assumed to be peripheral to the domain. Yet, this interpretation only holds if the definition of the domain is not contested by different groups of respondents. This could happen if we unwittingly mix respondents from very different cultures. For example, Chavez (1995) observed strong differences in freelisting responses by Mexicans, Salvadoreans, Chicanos, Anglos and Anglo physicians.

We can record the proportion of respondents placing each pair of items in the same pile using an item-by-item matrix, as shown in Table 4. This matrix can then be represented spatially via non-metric multidimensional scaling, or analyzed via cluster analysis.(8) Figure 5 shows a multidimensional scaling of pilesort similarities among 30 crimes collected by students of Mark Fleisher(9). In general, the purpose of such analyses would be to (a) reveal underlying perceptual dimensions that people use to distinguish among the items, and (b) detect clusters of items that share attributes or comprise subdomains.
Let us discuss the former goal first. One way to uncover the attributes that structure a cultural domain is to ask respondents to name them as they do the pilesort(10). One approach is to ask respondents to "think aloud" as they do the sort. This is useful information but should not be the only attack on this problem. Respondents can typically come up with dozens of attributes that distinguish among items, but it is not easy for them to tell you which ones are important. In addition, many of the attributes will be highly correlated with each other if not semantically related, particularly as we look across respondents. It is also possible that respondents do not really know why they placed items into the piles that they did: when a researcher asks them to explain, they cannot directly examine their unconscious thought processes and instead go through a process of justifying and reconstructing what they must have done. For example, all native speakers of a language are good at constructing grammatically well-formed sentences, but they need not have any conscious knowledge of grammar to do this.
In addition, it is possible that the research objectives may not require that we know how the respondent completes the sorting task but merely that we can accurately predict the results. In general, scientists build descriptions of reality (theories) that are expected to make accurate predictions, but are not expected to be literally true, if only because these descriptions are not unique and are situated within human languages utilizing only concepts understood by humans living at one small point in time. This is similar to the situation in artificial intelligence where if someone can construct a computer that can converse in English so well that it cannot be distinguished from a human we will be forced to grant that the machine understands English, even if the way it does it cannot be shown to be the same as the way humans do it. What is common to both scientific theories and artificial intelligence is that we evaluate truth (success) in terms of the behavioral outcomes, not an absolute yardstick.
To discover underlying dimensions we begin by collecting together the attributes elicited directly from respondents. Then we look at the MDS map to see if the items are arrayed in any kind of order that is apparent to us.(11) For example, in the crime data shown in Figure 5, it appears that as we move from right to left on the map, the crimes become increasingly serious. This suggests the possibility that respondents use the attribute "seriousness" to distinguish among crimes. Of course, the idea that the leftmost crimes are more serious than the rightmost crimes is based on the researcher's perceptions of the crimes, not the informants'. Furthermore, there are other attributes that might arrange the crimes in roughly the same order (such as violence). The first question to ask is whether respondents have the same view of the domain as the researchers.
To resolve this issue, we then take all the attributes, both those elicited from respondents(12) and those proposed by researchers, and administer a questionnaire to a (possibly new) sample of respondents asking them to rate each item on each attribute. This way we get the informants' views of where each item stands on each attribute. Then we use a non-linear multiple regression technique called PROFIT (Kruskal and Wish, 1975) to statistically relate the average ratings provided by respondents to the positions of the items on the map. Besides providing a statistical test of independence (to guard against the human ability to see patterns in everything), the PROFIT technique allows us to plot lines on the MDS map representing the attribute so that we can see in what direction the items increase in value on that attribute. Often, several attributes will line up in more or less the same direction. These are attributes that have different names but are highly correlated. The researcher might then explore whether they are all manifestations of a single underlying dimension that respondents may or may not be aware of.
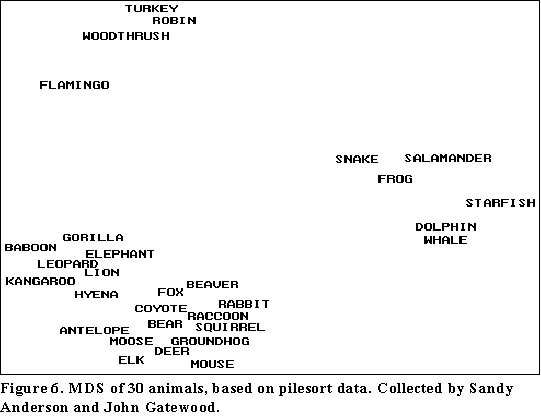
Sometimes MDS maps do not yield much in the way of interpretable dimensions. One way this can happen is when the MDS map consists of a few dense clusters separated by wide open space. This can be caused by the existence of sets of items that happen to be extremely similar on a number of attributes. Most often, however, it signals the presence of subdomains (which are like categorical attributes that dominate respondents' thinking). For example, a pilesort of a wide range of animals, including birds, land animals, and water animals will result in tight clumps in which all the representatives of each group are seen as so much more similar to each other than to other animals that no internal differentiation can be seen. An example is given in Figure 6. In such cases, it is necessary to run the MDS on each cluster separately. Then, within clusters, it may be that meaningful dimensions will emerge.
We may also be interested in comparing respondents' views of the structure of a domain. One way to think about the pilesort data for a single respondent is as the answers to a list of yes/no questions corresponding to each pair of items. For example, if there are N items in the domain, there are N(N-1)/2 pairs of items, and for each pair, the respondent has either put them in the same pile (call that a YES) or a different pile (call that a NO). Each respondent's view can thus be represented as a string of ones and zeros. We can then, in principle, compare two respondents' views by correlating these strings.
However, there are problems caused by the fact that some people have more piles than others. This is known as the "lumper/splitter" problem. For example, suppose two respondents have identical views of what goes with what. But one respondent makes many piles to reflect even the finest distinctions (he's a "splitter"), while the other makes just a few piles, reflecting only the broadest distinctions (she's a "lumper"). Correlating their strings would yield very small correlations, even though in reality they have identical views. Another problem is that two splitters can have fairly high correlations even when they disagree a great deal because both say "no" so often (i.e., most pairs of items are NOT placed in the same pile together). Some analytical ways to ameliorate the problem have been devised, but they are beyond the scope of this chapter.
The best way to avoid the lumper/splitter problem is to force all respondents to make the same number of piles. One way to do this is to start by asking them to sort all the items into exactly two piles, such that all the items in one pile are more similar to each other than to the items in the other pile. Record the results. Then ask the respondents to make three piles, letting them rearrange the contents of the original piles as necessary.(13) The new results are then recorded. The process may be repeated as many times as desired. The data collected can then be analyzed separately at each level of splitting, or combined as follows. For each pair of items sorted by a given respondent, the researcher counts the number of different sorts in which the items were placed together. Optionally, the different sorts can be weighted by the number of piles, so that being placed together when there were only two piles doesn't count as much as being placed together when there were 10 piles. Either way, the result is a string of values (one for each pair of items) for every respondent, which can then be correlated with each other to determine which respondents had similar views.
A more sophisticated approach was proposed by Boster (1994). In order to preserve the freedom of a free pilesort while at the same time controlling the lumper/splitter problem, he begins with a free pilesort. If the respondent makes N piles, the researcher then asks the respondent to split one of the piles, making N+1 in total. He repeats this process as long as desired. He then returns to the original sort and asks the respondent to combine two piles so that there are N-1 in total. This process is repeated until there are only two piles left.
Both of these methods, which we can describe as successive pilesorts, yield very rich data, but they are time-consuming and can potentially require a lot of time to record the data (while the respondent looks on). In Boster's method, because piles are not rearranged at each step, it is possible to record the data in an extremely compact format without making the respondent wait at all. However, it requires extremely well-trained and alert interviewers to do it.
6. The number 30 is merely a convention -- a rule of thumb. More respondents is always more desirable but involves more time and expense.
7. This means that there is a 1-to-1 correspondence between the rank orders of the data. That is, the pair placed most often in the same pile is the most similar, the pair placed second-most often in the same pile is the second-most similar, etc.
8. An excellent introduction to multidimensional scaling is provided by Kruskal and Wish (1978). For an introduction to cluster analysis, I recommend Everitt (1980).
9. The data were collected specifically for inclusion in this chapter by: Jennifer Teeple, Dan Bakham, Shannon Sendzimmer, and Amanda Norbits. I am grateful for their help.
10. It is best to use a different sample of respondents for this purpose, or wait until they have finished the sort and then ask them to discuss the reasons behind their choices. Otherwise, the discussion will influence their sorts. You can also have them sort the items twice: the first time without interference, the second time discussing the sort as they go. The results of both sorts can be recorded and analyzed, and compared.
11. It is important to remember that since the axes of MDS pictures are arbitrary, dimensions can run along any angle, not just horizontal or vertical.
12. Either as part of the pilesort exercise, or by showing the MDS map to informants and asking them what to make of it.
13. An alternative here is to ask them to divide each pile in two. This is repeated as often as desired.