M.G. Everett
School of Computing and Mathematical Sciences
University of Greenwich
Wellington Street
London SE 18 6PF

S.P. Borgatti
Organization Studies Dept.
Carroll Graduate School of Management
Boston College
Chestnut Hill, MA 02167

This paper extends the standard network centrality measures of degree, closeness and betweenness to apply to groups and classes as well as individuals. The group centrality measures will enable researchers to answer such questions as ‘how central is the engineering department in the informal influence network of this company?’ or ‘among middle managers in a given organization, which are more central, the men or the women?’ With these measures we can also solve the inverse problem: given the network of ties among organization members, how can we form a team that is maximally central? The measures are illustrated using two classic network data sets. We also formalize a measure of group centrality efficiency, which indicates the extent to which a group’s centrality is principally due to a small subset of its members.

Network analysts have used centrality as a basic tool for identifying key individuals in a network since network studies began. It is an idea that has immediate appeal and as a consequence is used in a large number of substantive applications across many disciplines. However, it has one major restriction: with few exceptions, all published measures are intended to apply to individual actors. It is a simple matter to think of areas of application that would benefit from a formulation that applies to groups of actors rather than individuals. Are the lawyers more central than the accountants in a given organization’s social network? Is one particular ethnic minority more integrated into the community than another? To what extent are particular groups or classes (women, the elderly, African-Americans, etc.) marginalized in different networks? All of these questions could be answered to some extent by the application of a centrality measure that applied to a set of individuals rather than a single individual.

In addition to a priori groups like the ones mentioned above, a group centrality measure could also be applied to sets of individuals identified by cohesive subgroup techniques (e.g., cliques), or by positional analysis techniques, such as structural equivalence or regular equivalence. For example, if applied to cliques in very large networks, we could use group centrality to identify which of many hundreds of cliques were the most important (in a well-specified sense) and should be analyzed more fully.

Another application of a group centrality measure would be as a criterion for forming groups. That is, we can write an algorithm to construct a set of groups, optionally mutually exclusive, that have maximal group centrality. Or, less ambitiously, a manager wanting to put together a team for a highly politically charged project might choose individuals who, in addition to having the appropriate skills, would also maximize the team’s centrality.

In order to develop a measure of group centrality we must first establish the criteria for success: the features and properties that we would like such a measure to possess. Our first requirement is that a group centrality measure be derived from existing individual measures. There are more than enough measures of centrality already in the literature, and we do not intend to introduce any more. Hence, what we introduce is a general method for applying existing measures to the group context, rather than new conceptions of centrality. Our second requirement is that any group measure be a proper generalization of the corresponding individual measure, such that when applied to a group consisting of a single individual, the measure yields the same answer as the individual version. An immediate consequence of this requirement is that we do not measure group centrality by computing centrality on a network of relationships among groups. Instead, the centrality of a group is computed directly from the network of relationships among individuals. A side benefit of this approach is that there are no problems working with overlapping groups, where one individual can belong to many groups.

An obvious approach to measuring group centrality would be to average or sum the individual centrality scores of group members (possibly disregarding ties to other group members). This approach has a number of problems. In a competitive situation, groups may form which seek to gain an advantage by having high centrality scores. Clearly it would de disadvantageous for the individual with the highest centrality to join with anyone else since the group centrality score would almost certainly be lower. More generally if a group had an average centrality score and an individual wanted to join them, unless the scores were equal, either the group should reject the individual or the individual should reject the group. This problem would also prevent us from achieving one of our goals, namely to allow us to use the measure as a criterion for forming groups. Another problem with using an averaging method is that it takes no account of the fact that actors may be central to (connected to) the same or different actors. For example, suppose we have a group X with a certain group centrality score and two actors y and z, where y is central to the same actors as the group X but z is central to a different set of actors. If y and z have the same centrality score, then by the averaging method the groups X+y and X+z will also have the same score -- but clearly the X+z group should have a better score.

In this paper we consider four measures of centrality: degree, closeness, betweenness, and flow betweenness. For the sake of clarity of exposition, we shall assume that the data consist of a connected, non-directed non-valued graph. However, the extension to non-symmetric and valued data does not present any special problems.

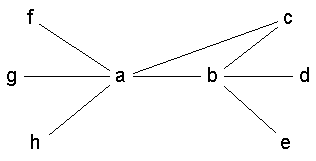
< Figure 1 >

Degree. We define group degree centrality as the number of non-group nodes that are connected to group members. Multiple ties to the same node are counted only once. Hence, in Figure 1, the centrality of the group consisting of nodes a and b is 6. We can normalize group degree centrality by dividing the group degree by the number of non-group actors. Hence, the normalized degree centrality of the group {a,b} is 1.0.

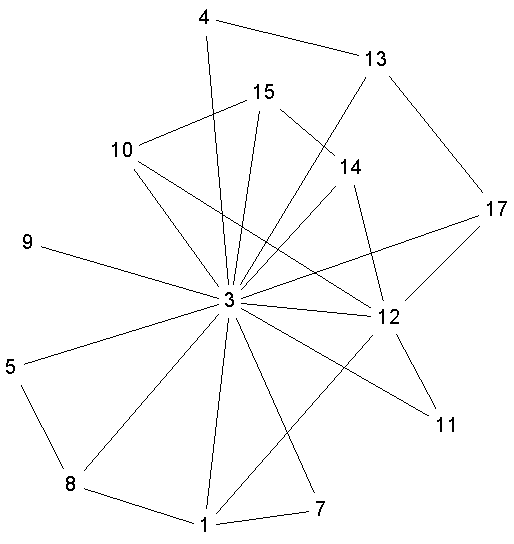
< Figure 2 >

As an example of group centrality we shall look first at the primate data collected by Linda Wolfe and given as a standard dataset in UCINET (Borgatti, Everett and Freeman 1992). The data records 3 months of interactions amongst a group of 20 monkeys, where interactions were defined as joint presence at the river. The dataset also contains information on the sex and age of each animal. We shall consider six different groups. The first two groups will be formed by sex; the remaining four will be formed by age. The purpose of dividing them by age is merely a device to illustrate the techniques in this paper and we should emphasize that we have no substantive reason for these groupings. The data is symmetric and valued and we have dichotomized it by taking the presence of a tie to be more than 6 interactions over the time period (see Figure 2).

Table 1. Individual Centrality Scores

Table 1 gives the individual centralities for each monkey on four centrality measures, including both normalized and un-normalized versions. Table 2 gives the group degree centrality and normalized group degree centrality for the six groups.

Among the age groups, the most central group is clearly the 10-13 year olds. This is the group that contains monkey 3, who (as shown in Table 1) is highly central as an individual. The effect of normalization is readily apparent in comparing groups 3 and 4: they have the same raw group centrality score but group 3 is more central once the data have been normalized. The effect is even more dramatic when we look at the male and female groups. Un-normalized, the males are clearly more central than the females. But normalized, the situation is reversed. It is clearly easier for larger groups to achieve higher normalized centrality scores than smaller groups because they contain more individuals to connect with a smaller outside group. We shall return to this point in the next section. Normalization has greater significance in group centrality than in individual centrality. This is because the differing sizes of groups mean that the transformation is non-linear and hence the rank order of the normalized group centralities can be quite different from the un-normalized ones.

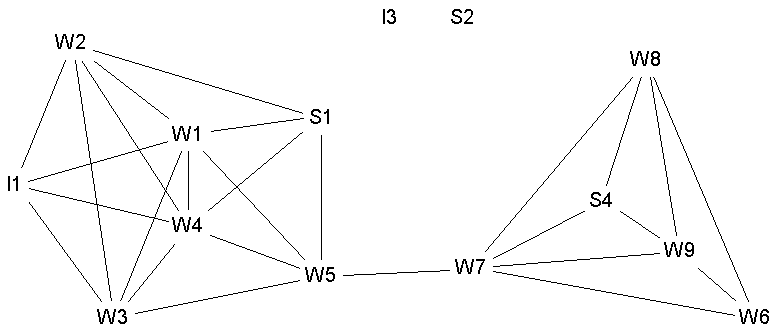
< Figure 3 >

As we have already mentioned, we can use group centrality to examine emergent groups (revealed by standard network analysis procedures) as well as a priori classifications. Our second empirical example uses the Bank Wiring Room data of Roethlisberger and Dickson (1939), available in UCINET as well. In particular we examine the Games matrix (see Figure 3). Isolates I3 and S2 were deleted before performing any analysis. A clique analysis of these data finds 5 cliques with a considerable amount of overlap of the groups. Table 3 gives the group degree and normalized group degree centrality for the cliques together with the members of the groups.

Clearly, clique 3 has the highest group centrality score, but all the values are fairly similar. The first three groups are all the same size, and therefore, among those three, the raw and normalized scores are proportional to each other.

There is an important point to be considered when we use the concept of group degree centrality on cohesive subgroups. To some extent, the notion of a cohesive subgroup includes the idea of many links within the group, and few links to outsiders (Borgatti, Everett and Shirey, 1991). Indeed, certain types of cohesive subsets (e.g., LS sets) are explicitly constructed in such a way that they must have weak links to the rest of the network. Such groups necessarily have low group degree centrality. Groups that have high degree centrality are groups with highly porous or ambiguous boundaries.

Closeness. We can define group closeness as the sum of the distances from the group to all vertices outside the group. As with individual closeness, this produces an inverse measure of closeness as larger numbers indicate less centrality. This definition deliberately leaves unspecified how distance from the group to an outside vertex is to be defined. This problem has been well researched in the hierarchical clustering literature (Johnson, 1967) and we propose to adopt their methods. Consider the set D of all distances from a single vertex to a set of vertices. We can define the distance from the vertex to the set as either the maximum in D, the minimum in D or the mean of values in D. For example, in Figure 2, the group consisting of {8,1,7} is distance 1 from node 12 via the minimum method (because node 1 is just one link away from 12), distance 2 from 12 via the maximum method (because both nodes 7 and 8 are two links from 12), and distance 1.67 via the mean method (because the average distance is (2+2+1)/3). Of course, when the group consists of a single node, all of these distances are identical and the group centrality is the same as individual centrality.

Following Freeman’s (1979) convention, we can normalize group closeness by dividing the distance score into the number of non-group members, with the result that larger numbers indicate greater centrality. Tables 4 and 5 give the group closeness for the primate and games data using the same group numbering as before. In the primate data we have permanently deleted the isolates 2,6,16,18, 19 and 20, and in the Games data we have deleted the two isolates I3 and S2.

As can be seen in Table 4, the minimum method does not provide much sensitivity: it is relatively easy to attain the maximal value. In contrast, the maximum method is the most stringent method, yielding the smallest value in all cases. The maximum and minimum methods are similar in the sense that in both methods the distance of an individual to the group is defined by the distance to a specific group member (either the closest or the furthest). In contrast, the average method defines the distance in terms of all group members.

The choice of method for a given application will depend on the circumstances. If it is thought that the group, once formed, acts as a single unit, then the minimum method is appropriate. In a sense, the minimum method ignores internal structure (in particular, distances), and is therefore almost equivalent to collapsing the group down to a single node whose ties are the union of the ties to outsiders possessed by members. This may be appropriate when forming the group yields a qualitatively different kind of agent, such as a corporation or other legal entity. Another situation in which the minimum method might be appropriate is a communication network in which cohesive groups have been identified consisting of individuals who have worked together closely for many years, learning each other’s ways and developing the ability to communicate with extraordinary efficiency. Even though individuals within the group are separated by a link (i.e., they are still separate individuals), communication across internal links is virtually instantaneous and complete, and so here again it is appropriate to ignore internal structure. In contrast, when internal communication is not particularly good (or totally non-existent, as could occur with classes defined on attributes), and it is important that all members of the group have received all information, then the maximum method may be more appropriate. When the rules of information transmission in the network suggest that a node transmits information to a randomly chosen node in its neighborhood, the average method may be the best choice, as the expected time-until-arrival of a message to the group will be a function of all the distance from group members to all other nodes in the network.

Comparing the group closeness results with the group degree results we see a broad agreement between the measures across both data sets. The only striking difference is in the centrality of the male monkeys, where using the maximum method they are the least central of all the groups. This is because they contain an individual placed slightly further away than the others all of whom are very central. The minimum method will ignore him, the average method ameliorates the effect, while the maximum method exposes the situation.

Betweenness. We now examine the third classic centrality measure, betweenness. The properties of betweenness are radically different from those of degree and closeness and the results are often correspondingly different. Let C be a subset of a graph with vertex set V. Let g_u,v be the number of geodesics connecting u to v and g_u,v(C) be the number of geodesics connecting u to v passing through C. Then the group betweenness centrality of C denoted by C_B(C) is given by

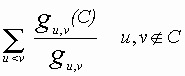
In other words the group betweenness centrality measure indicates the proportion of geodesics connecting pairs of non-group members that pass through the group. One way to compute this measure is as follows: (a) count the number of geodesics between every pair of non-group members, yielding a node-by-node matrix of counts, (b) delete all ties involving group members and redo the calculation, creating a new node-by-node matrix of counts, (c) divide each cell in the new matrix by the corresponding cell in the first matrix, and (d) take the sum of all these ratios.

As with individual betweenness centrality, we can normalize group betweenness by dividing each value by the theoretical maximum. The theoretical maximum occurs for a group of a given size when the result of identifying all the group vertices (i.e. shrinking them to a single vertex) is a star with the group in the center. We therefore define the normalized group betweenness centrality C¢ _B(C) as

C¢_B(C) = 2 C_B(C)/(½ V½ -½ C½ )(½ V½ -½ C½ -1)

Tables 6 and 7 give the group betweenness scores for the primate and games data.

In examining the group betweenness results we notice that three of the groups have a value of zero. It should be noted that only one of these groups consists of individuals all of whom have individual betweenness centrality of zero – by joining a group, some individuals may "lose" centrality. For the primate data we note the high scores achieved by group 2 and the male group. If we look at individual betweenness for these data (see Table 1), we find that only six monkeys -- 1,3,8,12,13 and 15 -- have non-zero betweenness. Of these, monkey 3 has by far the highest score. Clearly groups that contain individuals with high individual centrality scores inherit some of these scores, but not if the high scores were due to their connections with other group members. Thus, there is a sense in which individuals can enhance their betweenness scores by joining with individuals outside their own social circles.

Flow Betweenness. The fourth standard centrality measure is flow betweenness (Freeman, Borgatti and White 1991). Individual flow betweenness can be extended to group flow betweenness in the same way as ordinary betweenness. To calculate the group flow betweenness of a group C, first calculate the sum of maximum flows in the network between all pairs of vertices not in C. Call this quantity DEN. Then delete all ties involving nodes in C and repeat the calculation, calling the result NUM. Finally, divide NUM by DEN. It should be noted that group flow betweenness is quite a natural generalization of individual flow betweenness since the computational algorithm we have presented is precisely the algorithm used for individual flow betweenness (Borgatti, Everett and Freeman, 1992), where C contains just one vertex.

4 Efficiency

As we have already remarked, larger groups find it easier to get higher normalized group centrality scores since they have to be central to (connected to) a smaller outside group. If we were to look at the inverse of the problem we have been addressing so far, namely, given a network, find a group with maximum group centrality, then we would quickly find it attractive to look for large groups. Consider degree centrality: if we take any non-isolated vertex and place all other vertices in a group, the group will have a normalized group degree centrality of one (an example is provided by nodes a through g in Figure 1). The same would apply to the minimum option in the group closeness measure. For betweenness we need to identify two non-adjacent non-isolated vertices (such as g and d in Figure 1) and place all the other vertices in a group. This group now has the maximum possible group betweenness score. Hence, by choosing large groups, we can almost always maximize group centrality.

However, notice that in larger groups most individuals are not contributing directly to the group centrality score. Their only contribution is to not be outside the group and therefore they do not have to be included in the computation, which means they only contribute indirectly. The presence of non-contributing members in a group suggests the concept of efficiency: the proportion of actors within the group who directly contribute to the centrality of the group. Of course, this conception of efficiency only makes sense for those centrality measure with the property that adding actors to the group cannot decrease the centrality score. We now formalize these concepts.

Degree, minimum closeness, betweenness and flow betweenness are all monotone group centrality measures and so we can define efficiency when we use them. The average and maximum closeness measures are not monotone hence efficiency is not defined for those measures. For example, consider the clique {W1, W3, W4, W5, S1} of the Games data (see Figure 3). The centrality of the group using the maximum method is 18. But the centrality of actor W5 is 13, which is considerably better than the whole group. Clearly, we cannot measure the contribution of W5 to the whole group since their individual contribution exceeds that of the whole group, it follows that, in these circumstances, efficiency as we have developed it cannot be applied. We note that any averaging method used to define group centrality would not be monotone and consequently we would not be able to examine efficiency. Monotonicity is an important property of group centrality and non-monotone methods should be used with extreme caution. This is another reason that we do not advocate taking the average centrality score of a group as a means of defining group centrality.

Table 8 gives the efficiency measure for each of the group centralities for the games data. Note that betweenness efficiency for the first clique has not been computed since the betweenness of the group is zero.

For degree and closeness, the combination of several poorly connected actors and one or two well-connected actors in a group means that the efficiency of the group must be low. However, for betweenness centrality, the situation is quite different. The presence of an extremely central member does not necessarily reduce group efficiency by making other nodes redundant. For example, in Clique 3 of the Games data, actor W5 has enormous individual betweenness. But he is in fact the one member of the clique that is expendable in the special sense that a subset of Clique 3 that does not include him (namely, the subset K = {W1 W3 W4 S1}), achieves full contribution as defined above.

As already mentioned, we could use the definition of group centrality as a basic tool to find important subgroups within a given network. A manager who wishes to introduce some new practices within an organization may wish to identify a well-connected subgroup that can develop and champion the cause. This subgroup would need to have a very high group centrality score. Yet to be effective, it would be desirable for the group to be as small as possible without sacrificing centrality. We could therefore search for a minimal subgroup with maximal group centrality.

For closeness or degree group centrality this would amount to finding the smallest group of actors within the network such that every actor outside the group is adjacent to a member of the group. This is a standard concept in graph theory, where the size of such a group is called the domination number of a graph (Carre 1979). We may not have such a stringent requirement and may only demand a group centrality greater than a certain value. Alternatively we may wish to find a group with a fixed size which has the maximum group centrality. Or we may wish to find a set of (possibly mutually exclusive) groups that, overall, maximize centrality. Any of these searches amount to searching all subgroups for the group or groups which best fit the required conditions. These therefore fall into the category of combinatorial optimization problems and can be solved by any of the standard heuristic methods such as a genetic algorithm (Holland 1975).

We can perform such a search on the Games data. The domination number for the Games graph is 2, and this can be achieved with a number of different pairs, including {W1, W7}, {W1, W8}, and {W1, W9}. As we have already noted, the maximal betweenness occurs when the group forms the center of a star. This can always be achieved by a group smaller than the whole group, provided we do not have a complete graph. In the Games data, the smallest group with maximal betweenness is surprisingly large (size 8), and there are three of these. One example is {I1,S1,W1,W3,W4,W7,W8,W9}. This example is interesting because it does not contain the highly central actor W5, although there is an alternative group of the same size which does contain him.

The methods and principles of the paper represent just one of a number of approaches that could be taken to defining group centrality. In this section we briefly outline an alternative and discuss some associated problems and advantages of this approach.

An intuitively obvious approach is to replace all the members of a group by a single "super" vertex whose neighborhood is the union of the neighborhoods of all group members. That is, there is a connection from the new vertex to another vertex if there was at least one actor in the group who had that connection. If G was the original graph, then we call the new graph the group reduced graph denoted by G*. If G had n actors and a group C had c actors then G* contains n-c+1 actors. We could then submit G* to any standard individual centrality routine to obtain the centrality measure for the group. This procedure would give exactly the same results for degree centrality as we obtained using our group degree centrality measure. If we apply closeness centrality to G* then we obtain the same results as the group closeness measure based on the minimum method. We cannot, however, reproduce the mean and maximum closeness methods using this technique.

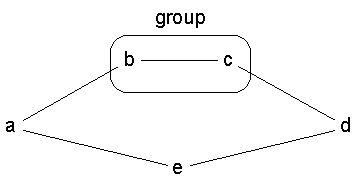
< Figure 4 >

Differences also occur when we apply the betweenness centrality measure. The reason is that the internal structure of the group has no effect on the reduced model, but does affect the group betweenness measure we defined earlier. In the reduced model, connections internal to the group do not exist, so geodesics passing through the group can be shorter. An example is shown in Figure 4. Using our original group betweenness measure, the centrality of the group {b, c} is zero, as the internal link increases the length of the path from a to d passing through the group to 3 links, which is longer than the geodesic distance of 2.

The fact that, in the reduced model, the internal cohesion of a group does not affect its centrality, is an important conceptual advantage of the reduced model. There are practical benefits as well. In the earlier model, if the individual betweenness of each member of a group is zero, the centrality of the group must be zero as well, much like the averaging method. Therefore, for completely peripheral individuals, there is no strategic benefit to forming a group. In contrast, using the reduced model approach, the centrality of the group in Figure 4 is 0.5, as there are now two geodesics from a to d, and one of them passes through the group. This approach therefore lends itself to a more strategic view of group formation, perhaps based on a rational actor model. For example, a peripheral actor in a communication network might seek to increase their betweenness centrality by partnering with other peripheral actors, such that the combination has high centrality. This assumes, of course, that once actors are teamed, communication among members is complete and instantaneous.

Tables 9 and 10 give the results of the reduction method on our two data sets using betweenness centrality. For the Games data, the betweenness scores were exactly the same as using the original group betweenness definition. This is not the case for the primate data. We can see in Table 10 that all the group centrality scores have increased and two of the groups that had a zero score now have a positive betweenness value.

Another advantage of the reduced graph approach is that it allows us to construct group versions of any centrality measure, including ones that are difficult to generalize along the lines presented earlier in this paper. An example of such a measure would be eigenvector centrality (Bonacich, 1972). Eigenvector centrality is defined as the principal eigenvector of the adjacency matrix for the graph. As such, it is virtually impossible to generalize along the lines presented earlier, but easy to handle via the reduced graph approach.

The basic criticism of the reduced graph method is that the removal of the internal links in a group is hard to justify substantively. If in the network in general the links represent communication channels among actors, and if longer paths take longer to traverse (or involve decay of usable information), how is it that, by forming a group, these basic laws of propagation are suspended within the group? It is hard to imagine what substantive processes might correspond to these algorithmic procedures.

Another recent stream of research has focussed on strategic networking, particularly at the individual level (Burt 1992; Baker 1994). For example, Burt (1992) considers how to evaluate potential partners so as to maximize the reach of an actor’s ego network. Computationally, the problem is equivalent to finding a maximally central subset of actors that include ego. An interesting line of research would be to discover the conditions under which individuals’ sociometric choices do or do not accord with strategic principles (i.e., maximizing ego network centrality). For example, we might expect that business contacts conform to strategic principles while friendship contacts do not. Conversely, from a consulting or prescriptive point of view, group centrality measures may provide a guide for selecting partners, either among persons or corporations.

Group centrality measures may also provide an avenue for defining or operationalizing substantive concepts. For example, the notion of a core/periphery structure is prevalent in many literatures (notably the study of elites and in world systems theory). But no formal definition of a core (or periphery) has been proposed. Given the existence of group centrality measures, it would be quite natural to define the core of a network as that subset of actors whose group centrality is greater than all others. Another example of operationalizing fundamental constructs is provided by the notion of ‘social capital’. Social capital has come to mean many very disparate things, but one of them is surely the set of benefits that accrue from the set of ties that an individual or group possesses with others in the network. Group centrality measures clearly provide a way to operationalize this aspect of the concept of social capital.

Baker, W. E.1994 Networking smart : how to build relationships for personal and organizational success. New York : McGraw-Hill

Bonacich, P.1972 Factoring and weighting approaches to status scores and clique identification. Journal of Mathematical Sociology 2:113-120.

Bonacich, P.1991 Simultaneous group and individual centralities. Social Networks 13(2):155-168.

Borgatti, S.P., M.G. Everett and L.C. Freeman1992 UCINET, Version IV. Columbia, SC: Analytic Technologies

Carre, B.1979 Graphs and Networks. Oxford: The University Press.

Freeman, L.C., S.P. Borgatti and D.R. White 1991 Centrality in valued graphs: A measure of betweenness based on network flow. Social Networks 13: 141-154.

Geletkanycz, M. A. and D.C. Hambrick. 1997 The External Ties of Top Executives: Implications for Strategic Choice and Performance. Administrative Science Quarterly. In press.

Holland, J.H.1975 Adaptation in natural and artificial systems. Ann Arbor : The Univ. of Michigan Press.

Roethlisberger, F.J. and W.J. Dickson. 1939 Management and the Worker. Cambridge, MA: Harvard University Press.