Analyzing Clique Overlap

The identification of cohesive areas of a network has been the goal of many social network analyses. Techniques have been taken from multivariate statistics (MDS, clustering etc.) as well as from graph theory. The multivariate techniques are often used as additional processing on the outcome of some other network-analytic procedure (e.g. role analysis or geodesic distances). In contrast, researchers working directly with raw data typically use methods based on the deterministic definitions of graph theory. In this paper we will only be concerned with these methods.

Deterministic definitions of cohesive subgraphs include: clique (Luce and Perry 1949), n-clique (Alba 1973), n-club, n-clan (Mokken 1979), k-plex (Seidman and Foster 1978), diplex (Seidman 1980), block, n-component, unilateral component, strong component, weak component, component (Harary, Norman and Cartwright 1965), LS-set (Luccio and Sami 1969), -set (Borgatti, Everett and Shirey 1990) and k-core (Seidman 1983). The last six of these definitions produce subgraphs which do not overlap and therefore are not the subject of this paper. The remaining nine definitions allow for actors to be members of more than one group. Clearly researchers selecting a particular method will take account of which methods produce overlapping groups and which will not. It is a simple matter to think of a large number of practical examples in which the expected norm is to have overlapping groups. Indeed the methods which do not allow for overlap may be viewed as odd since they place an artificial constraint on the groupings they are seeking to uncover.

For many of the methods mentioned in the last section, overlap can present serious problems in terms of interpreting the results. A 21 vertex graph can have as many as 2,187 cliques. While this represents an extreme situation and would never occur in real data it is an indication of the size of the problem. As a practical example Kapferer's Tailor shop data (Kapferer 1972 second time period) has just 39 actors and yields 118 cliques. There are very few techniques available to the researcher to try and help with interpreting the outcome of such an analysis. This paper tries to begin to address this problem. In the remainder of this paper, for simplicity we shall concentrate our attention on Luce and Perry (1949) cliques, but the ideas and methods we develop are generally applicable to any cohesive subgroup finder.

To aid in the analysis of overlap, UCINET provides an automatic analysis of the clique co-membership matrix first proposed by Lin Freeman. Define an n-by-n clique overlap matrix A, where A(i,j)=number of times i is in a clique with j. The ith diagonal entry gives the number of cliques containing i, which can be thought of as a measure of the centrality of i. This matrix is then submitted to a clustering algorithm to produce non-overlapping groups.

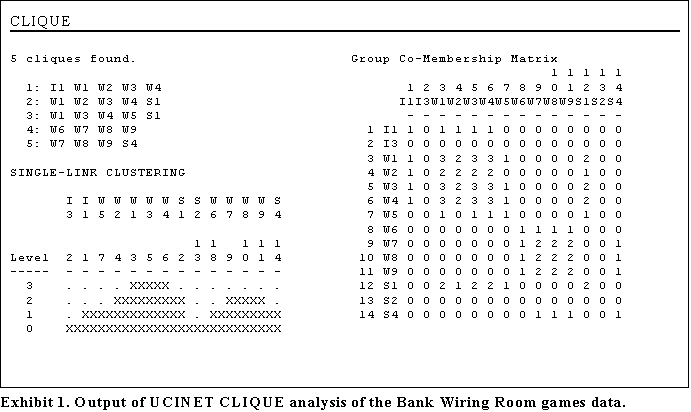
This method can be demonstrated by using the Games matrix from the Bank Wiring Room data (Roethlisberger and Dickson 1939) contained in UCINET . The UCINET output from the CLIQUE procedure is given in Exhibit 1.

The two groups {I1,W5,W2,W1,W3,W4,S1} and {W6,W7,W8,W9,S4} are clearly identified from the hierarchical clustering. These two groups correspond to the groupings identified by Roethlisberger and Dickson from direct observation. In addition, looking at the diagonal of the overlap matrix, we can pick out a few actors that are members of three cliques: W1, W3 and W4. These are high in "clique centrality", and it also happens that they are in the three cliques with each other, indicating that they form the core of a larger group. While, in this instance, the method identifies the two basic cohesive subgroups accurately it is not clear what the clusters represent in general. The clustering is based upon the activity of dyads and not on the strength or overlap of the cliques. A consequence of this is that it is biased towards a large number of overlapping cliques and therefore care needs to be exercised in interpreting any results. As an example consider the graph

, which is drawn in Figure 1.

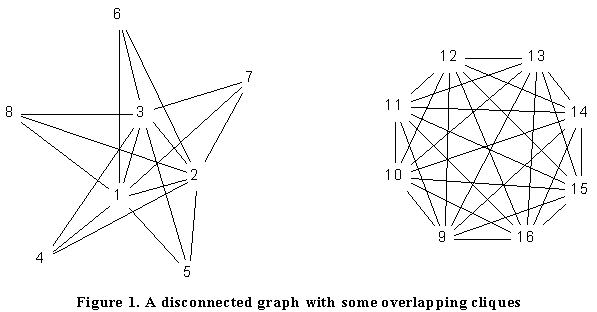
The graph contains 6 cliques and the hierarchical clustering of overlap is given in Exhibit 2.

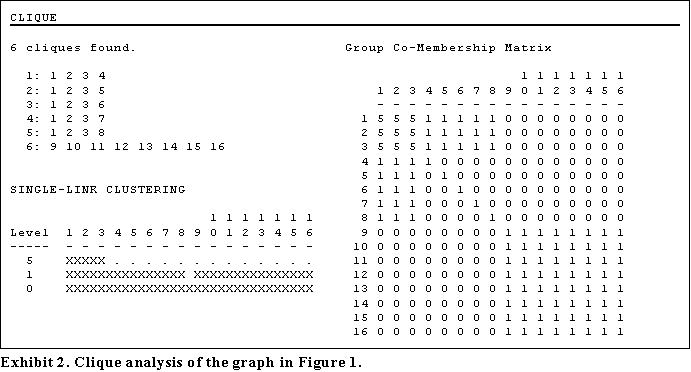
The clustering indicates a strong cohesive group 1,2,3 at level 5 and two larger weaker groups 1 to 8 and 9 to 16. The unsuspecting analyst may well draw a conclusion that the small group is a tightly integrated subgroup, which is by far the most important group in the network. The output gives little indication that there is a large strong group that may well dominate the network.

A different problem is that the method may fail to provide any insight at all into the clique structure of the network. It is possible for the clustering itself not to reveal any underlying structure. Consider the graph in Figure 2. The output of the UCINET clique analysis is shown in Exhibit 3.

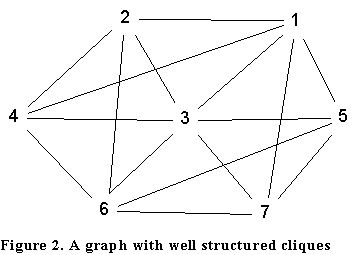
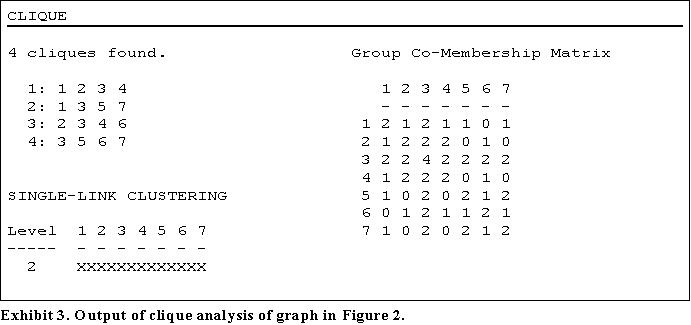
The single-link clustering has merged together all the cliques into one group. Whilst this could be cured by using a different clustering method it does demonstrate the care required in applying these methods. (It may be noted, however, that the diagonal of the clique overlap matrix nicely identifies node 3 as being highly central.)

Finally a problem with this method is that it removes one of the basic features of cohesive groups -- i.e., that they overlap. It seems counter-intuitive to solve the problem of too much overlap by removing it all. This amounts to throwing out the baby with the bath water. We now turn our attention to techniques which try and simplify the overlap -- without completely destroying it!

An alternative approach is to construct the intersection graph of the cohesive subgroups. This construction has the advantage of giving a pictorial representation of the clique structure which is not complicated by a further level of analysis. Let V₁, V₂.....V_k be a collection of cohesive subgroups of a network. The intersection graph has V₁, V₂....V_k as vertices with V_i and V_j adjacent if and only if they have a vertex in common. The intersection graphs for the cohesive subgroups identified in the Bank Wiring room data, Figure 1, and Figure 2 are given in Figure 3.

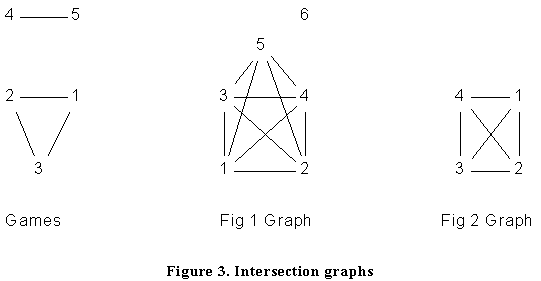
If in addition the cohesive subgroups are cliques then the intersection graph is called a clique graph. The clique graph of a graph G is denoted by K(G). The last two graphs in Figure 3 are clique graphs; strictly speaking, the first is not since we do not include all the cliques (we ignore those of size 1 and 2). A complete listing of the cliques for the Games matrix (we do, however, ignore the isolates I3 and S2) together with its clique graph is given in Figure 4.

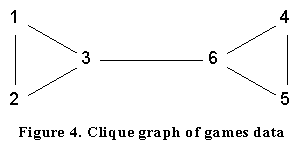
We note that the intersection graph for the Games matrix (left side of Figure 3) easily identifies the two major groupings since they are simply the components. The clique graph given in Figure 4 also can be used to identify the groups by either looking for cliques or bi-components. Clearly in the general case we can always look for cohesive groupings in the intersection or clique graphs to try and simplify the overlapping structures. For clique graphs there is a limit to the extent of any simplification. The following results are well known:

The notation d(G) indicates the maximum geodesic distance in a graph G, known as the diameter. The results imply that if we use clique graphs, it will always be more complicated than just finding the components to try and simplify the overlapping groups. The fact that the diameter does not change much indicates that the clique graph may not be much help. Mathematicians have made extensive studies of clique graphs. In particular they have looked at the question of when a graph is a clique graph of another graph and have also studied iterated clique graphs. We define the n^th iterated clique graph K_n(G) of a graph G inductively by

The study of iterated clique graphs by mathematicians has concentrated on two questions:

The second question has only recently been decided (in the affirmative). More information is contained in Larrion and Neumann-Lara (1997).

Clique graphs and iterated clique graphs still suffer from a number of problems. We note that the clique graph of the graph in Figure 2 does not help in our analysis (see right-hand side of Figure 3). Further the iterated clique graph K₂(G) is just a singleton. It is also possible for the clique graph to be the same as the original graph, a simple example is the cycle so that K(C_n)=C_n.

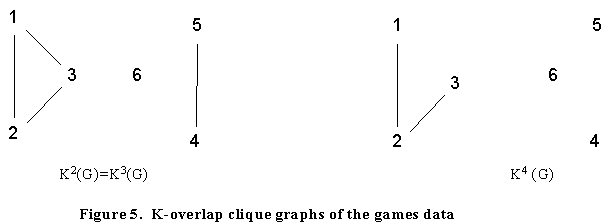
An alternative strategy to iterating the clique graph is to increase the amount of overlap between two cliques before they are considered to be adjacent. The k-overlap clique graph K^k(G) of a graph G is the graph whose vertices are the cliques of G, two vertices being adjacent if the corresponding cliques have k vertices in common. Clearly we can also perform a similar construction with any intersection graph. Figure 5 gives the k-overlap clique graphs for the Games data from the Bank Wiring room. It can be seen that K²(G) identifies the two major groupings that were not as clearly evident from the clique graph. In addition K⁴(G) shows the strong relationship between the first three cliques.

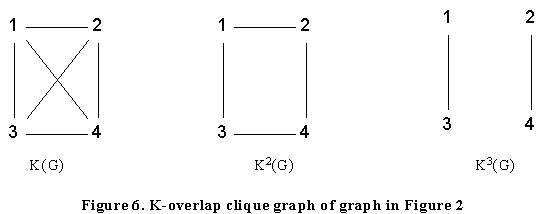
Applying the same technique to the graph in Figure 2 we obtain K²(G) and K³(G) as shown in Figure 6. In the figure, the components of K³(G) indicate that it could be meaningful to merge cliques 1 and 3; and 2 and 4. If we do this then we obtain the groupings {1,2,3,4,6}, {1,3,5,6,7}. We note that 1,3 and 6 are in both groups. We could conclude that 1,3 and 6 are the key actors and that 2,4,5 and 7 are less strongly involved. To test this claim we investigate the centrality of these actors. All centrality measures in UCINET give the highest centrality score to 3, followed by 1 and 6, the vertices 2,4,5 and 7 all have significantly lower scores. (Here again, we make the suggestion that the number of cliques that an actor is involved in is a potentially useful new measure of its centrality.)

It follows from all the above that examining clique and clique overlap graphs has allowed us to gain a greater insight into the cohesive subgroup structure of the original network. The major aim of this analysis should be in reducing the overlap between the cliques. The technique currently used in UCINET (i.e., hierarchical clustering based on the clique overlap matrix) assigns individual actors to unique groups. An alternative to this method suggested by the work above is that we should instead look at the dual formulation of clustering on the cliques rather than the actors. We form a matrix A called the co-clique matrix, the (i,j)^thentry of A is the number of actors clique i and clique j have in common. The diagonal entries give the size of the cliques. This matrix can then be submitted to any standard hierarchical clustering routine, the clusters will then assign each clique to a unique cluster. The result will be a series of nested groups of actors but actors will be able to appear in more than one group.

This analysis is simple to perform using UCINET by taking the clique by actor incidence matrix produced in all cohesive subgroup routines and submitting it to the AFFILIATIONS routine. The result of this can then be submitted to any of the hierarchical clustering methods. Exhibit 4 shows how the technique works on the Games data from the Bank Wiring room.

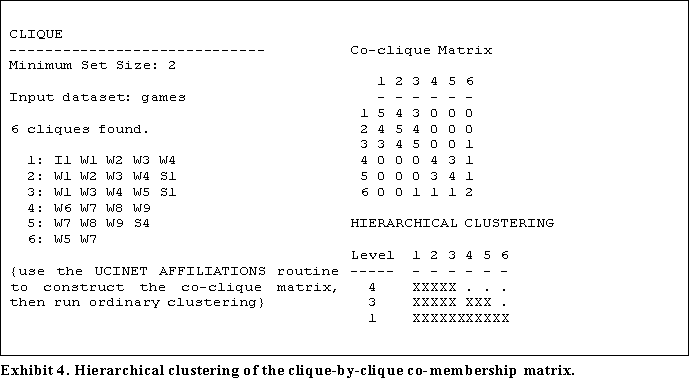
In the exhibit, the co-clique matrix is a clique-by-clique matrix indicating the number of actors each pair of cliques has in common. This is then submitted to hierarchical clustering. Clearly the method identifies the two groups; cliques 1, 2 and 3 correspond to {I1, W1,W2,W3,W4,W5,S1} and 4 and 5 correspond to {W6,W7,W8,W9,S4} repeating the analysis from the actor based method. Clique 6 is the bridge -- the only connection -- between these two groups.

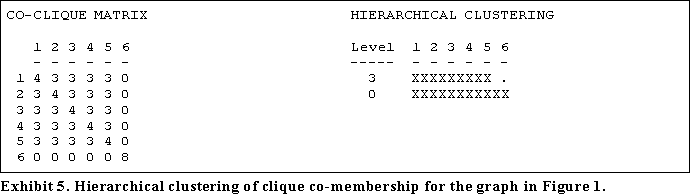
If we apply the technique to the graph in Figure 1 we obtain the results shown in Exhibit 5. The cliques 1 to 5 correspond to the actors 1 to 8 and clique 6 to actors 9 to 16. Actors 1, 2 and 3 are no longer singled out as a special group as in the actor-based overlap analysis. However, care is still required in interpreting the relative strengths of the two major groups.

The method will obviously replicate the iterated clique graph analysis for the graph in Figure 2 given in Figure 6 and will merge together the two pairs of cliques {1,3} and {2,4}.

For a more demanding test of the method we turn our attention to the Tailor Shop data mentioned earlier in this section. The data we consider consists of the two friendship matrices among the 39 actors that were taken at two time intervals seven months apart. The data are interesting because an abortive strike occurred after the first set of observations and a successful strike occurred after the second (Kapferer, 1972). A clique analysis yields 58 cliques after the first time period and 118 after the second. This clearly shows an increase in activity but a look at the standard overlap analysis reveals very little structure in the data and no difference except in volume between the two time periods. In contrast the co-clique analysis highlights some fundamental differences between the two matrices. Two groups can be identified which have (for these data) relatively little overlap. The first group consists of 9 actors and the second 10, the two groups have two actors in common (Chisokone and Mukubwa). In the second time period there are no separate groups and there is no partition of the cliques or actors as in the first time period. This indicates that there was a need to integrate the whole group to provide the necessary impetus for the strike. It should be further noted that the two actors in common between the two main groupings were highly active and were members of a large number of cliques.

The basic output of a clique analysis is an actor-by-clique incidence matrix X which indicates which actors belong to which cliques. As noted earlier, UCINET automatically generates a hierarchical clustering of XX' (an actor-by-actor matrix indicating the number of cliques that each pair of actors belong to in common). This paper has proposed an alternative, which is to analyze X'X (a clique-by-clique matrix which indicates the number of actors that each pair of cliques shares).

Since both XX' and X'X are of interest, it is logical to consider a singular value decomposition of X, which, in effect, analyzes both at the same time, generating a spatial representation that includes both the actors and the cliques they belong to. A sophisticated variant of this approach (correspondence analysis), transforms the data matrix prior to decomposition to remove the effects of the row and column marginals.

However, as noted by Borgatti and Everett (1997), correspondence analysis is not guaranteed to yield a useful 2-dimensional representation. For example, points widely separated on higher dimensions may have identical coordinates in the first two dimensions, causing them to be plotted right on top of each other on a 2-dimensional page of paper. An alternative is to use a combinatorial optimization algorithm such as simulated annealing to locate the points in such a way as to maximize legibility criteria. This capability is built into the Krackplot program, as described by McGrath, Blythe and Krackhardt (1996). The results of a Krackplot layout of the clique structure from the Games matrix of the Bank Wiring Room data, using a starting configuration computed via correspondence analysis, is shown in Figure 7.

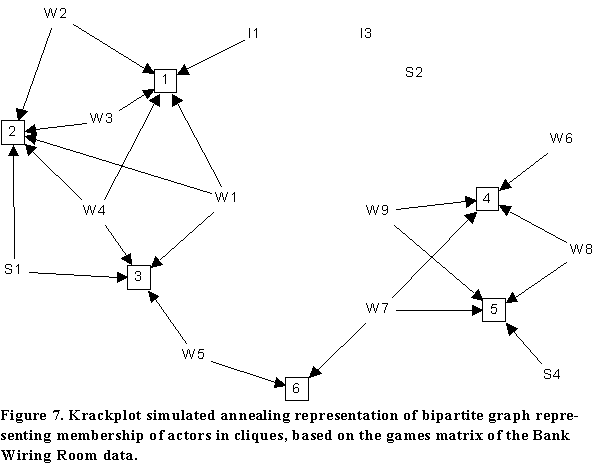
In the figure, the six cliques are represented by squares. The diagram makes it immediately obvious that the cliques {1, 2, 3} form one group, cliques {4, 5} form another, and clique 6 (with just two members, W5 and W7) is the bridge between the two groups. The diagram nicely highlights the bridging role played by W5 and W7, as well as the structural similarities between W9 and W8, as well as between W6 and S4.

We have mentioned a few times that the number of cliques that an actor belongs to could be seen as a new measure of centrality --- "clique overlap centrality". There are a number of intuitive rationales for this. For one thing, it is clear that highly peripheral points (isolates, pendants, etc.) will not belong to many cliques. The actors that belong to many cliques are actors located in the midst of dense knots of players. For another thing, actors with high clique overlap centrality are structurally important to the graph in the sense that removing them will tend to change the clique overlap structure dramatically.

The question naturally arises, then, 'How does clique overlap centrality relate to other measures of centrality?'. While we have yet to conduct a systematic investigation, it appears that for networks that generally conform to a core/periphery structure, clique overlap centrality correlates highly with most other measures, and particularly with degree and flow betweenness. An example is given by the Zachary (1977) Karate Club data. We computed the centrality of all 34 actors using 7 measures of centrality: clique overlap centrality, degree, normalized closeness, betweenness, eigenvector centrality, flow betweenness and information centrality. We then performed a correspondence analysis on the actor-by-measure matrix. The results are given in Figure 7.

In the plot, clique overlap centrality is labeled "CliqueOverlap", and the actors are labeled "R1" through "R34". As can be seen, clique overlap centrality is a fairly central measure, correlating especially well with degree and flow betweenness. It is also somewhat closely associated with nodes R1, R34 and R33, which were identified ethnographically by Zachary as leaders in the Karate Club.

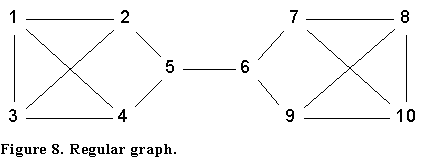
Of course, the correlations among measures of centrality change depending on the structure of the network. The network shown in Figure 8 is interesting in this regard. In this graph, all nodes have equal degree, so degree centrality and eigenvector centrality are constants. As shown in Table 1, all other measures except clique overlap centrality have nodes 5 and 6 as the most central, {2, 4, 7, 9} as the next most central, and {1, 3, 8, 10} as the least central. But clique overlap centrality is exactly the opposite, correlating with other measures at levels near -1.0.

Node	Clique Overlap	Degree	Norm. Closeness	Between	Eigen- vector	Flow Between	Infor- mation
1	2.00	3.00	34.62	0.33	0.32	3.00	0.67
2	1.00	3.00	42.86	6.00	0.32	6.00	0.72
3	2.00	3.00	34.62	0.33	0.32	3.00	0.67
4	1.00	3.00	42.86	6.00	0.32	6.00	0.72
5	0.00	3.00	52.94	20.33	0.32	25.00	0.90
6	0.00	3.00	52.94	20.33	0.32	25.00	0.90
7	1.00	3.00	42.86	6.00	0.32	6.00	0.72
8	2.00	3.00	34.62	0.33	0.32	3.00	0.67
9	1.00	3.00	42.86	6.00	0.32	6.00	0.72
10	2.00	3.00	34.62	0.33	0.32	3.00	0.67

In general, it appears that clique overlap centrality indicates embeddedness in dense regions of a network. In networks where there is just one such region (as in a core/periphery structure), clique overlap centrality correlates highly with other centrality measures (as do they with each other). But when the network consists of multiple clumps separated by structural holes, clique overlap centrality can be quite different from the other measures.

In this paper we have explored overlap in graph-theoretic formulations of cohesive subgroups. First we reviewed the method used automatically by UCINET, consisting of a hierarchical clustering of the actor-by-actor co-membership matrix. Then we discussed two techniques based on analyzing the clique-by-clique co-membership matrix, one using intersection graphs, and the other direct clustering of the "co-clique" matrix. A combination method, based on correspondence analysis, was also proposed. Finally, we examined the significance for actors of being involved in many different cliques.

Alba, R.D. 1973 A graph-theoretic definition of a sociometric clique. Journal of Mathematical Sociology 3:113-126.

Borgatti, S.P., M.G. Everett and L.C. Freeman. 1991 UCINET, Version IV. Columbia, SC: Analytic Technologies.

Borgatti, S.P., M.G. Everett and Shirey, P.R. 1990 LS sets, lambda sets, and other cohesive subsets. Social Networks 12: 337-358.

Borgatti, S.P. and M.G. Everett. 1997. Network analysis of 2-mode data. Social Networks 19(3):243-269.

Everett, M.G. and S.P. Borgatti. 1993 An extension of regular colouring of graphs to digraphs, networks and hypergraphs. Social Networks 15: 237-254.

Freeman, L.C. 1979 Centrality in social networks: I. Conceptual clarification. Social Networks 1:215-239.

Harary, F., R.Z. Norman and D.Cartwright. 1965 Structural Models: An Introduction to the Theory of Directed Graphs. New York: John Wiley and Sons.

Kapferer, B. 1972 Strategy and transaction in an African factory. Manchester: Manchester University Press.

Larrion and Neumann-Lara. 1997. Clique divergent graphs with unbounded sequences of diameters. (Unpublished Manuscript).

Luccio, F., and M. Sami. 1969. On the decomposition of networks into minimally interconnected networks. Transactions on Circuit Theory C.T. 16, 184-188

Luce, R.D. and A.D. Perry. 1949. A method of matrix analysis of group structure. Psychometrika. 20, 319-327

McGrath, C., J. Blythe and D. Krackhardt. 1996. Seeing groups in graph layouts. Connections 19(2):22-29.

Roethlisberger, F.J. and W.J. Dickson. 1939. Management and the Worker. Cambridge, MA: Harvard University Press.

Seidman, S.B. 1980. Clique-like structures in directed networks. Journal of Social and Biological Structures 3:43-54

Seidman, S.B. 1983. Network structure and minimum degree. Social Networks. 5, 269-287.

Seidman, S.B. and B.L. Foster. 1978. A graph-theoretic generalization of the clique concept. Journal of Mathematical Sociology. 6, 139-154.

Zachary, W. 1977. An information flow model for conflict and fission in small groups. Journal of Anthropological Research 33:452-473.

End Notes

1. Address mail to Martin G. Everett, Department of Mathematics, University of Greenwich. Email: M.G.Everett@greenwich.ac.uk.