| Teaching Corner |
|---|
CONNECTIONS 20(1):35-38
©1997 INSNA
Stephen P. Borgatti
Carroll School of Management, Boston College
In Structural Holes, Ron Burt (1992; 1995) describes a set of new measures based on ego networks. One key set of measures is concerned with the notion of redundancy. The general meaning of redundancy is clear: a person's ego network has redundancy to the extent that her contacts are connected to each other as well. However, the exact definition of the measures is shrouded in mathematical equations which are ambiguous at best.(1)
The purpose of this short note is to clarify how to compute the redundancy measures. At the end, I also comment briefly on the relationship between these measures and other well-known measures, such as ego-network density and betweenness centrality.
Burt defines the effective size of a person's ego network as
![]()
where
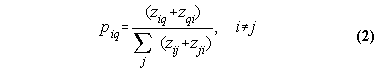
and
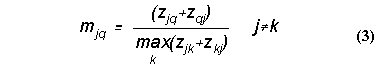
and Z is the data -- the matrix of network ties.
Let us assume that the network consists of a connected non-valued, undirected graph. That is, the data matrix Z contains only zeros and ones, and Z is symmetric so that zij equals zji. This allows us to simplify the math considerably. For example, Equation 2 becomes:
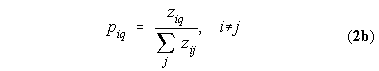
and Equation 3 becomes:
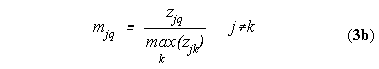
which further reduces to
![]()
since the maximum value Z will take on in a connected non-valued graph is necessarily 1.0.
This is an improvement, but before we do any calculating, we should be aware of one problem with these equations. Even though they are written in such a way as to yield a value for each node i in the network, these values are NOT correct for any node other than the center of the ego network. The reason is that Equation 1 contains nothing to exclude people (the j subscript) whom ego (the i subscript) has no relation to. This is works for the center of an ego network because the center is by definition tied to every other node, but fails for all other nodes. So the summation over j in Equation 1 has to be done just for those j's that are part of i's network. A quick and dirty fix for binary data is this:
![]()
By multiplying by mij, we only add in the quantity in brackets when ego is tied to that particular j.
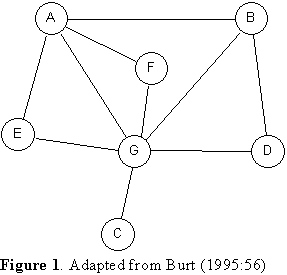
Consider the network in Figure 1. The first thing we want to do (Equation 2) is transform the data to be row-stochastic. That is, if node A is tied to 3 others, then we give each one a weight of 1/3. So we have a matrix P that looks like this:
Table 1. The row-stochastic P matrix.
| A | B | C | D | E | F | G | |
| A | 0.25 | 0 | 0 | 0.25 | 0.25 | 0.25 | |
| B | 0.33 | 0.0 | 0.33 | 0 | 0 | 0.33 | |
| C | 0 | 0 | 0 | 0 | 0 | 1.00 | |
| D | 0 | 0.50 | 0 | 0 | 0 | 0.50 | |
| E | 0.50 | 0 | 0 | 0 | 0 | 0.50 | |
| F | 0.50 | 0 | 0 | 0 | 0 | 0.50 | |
| G | 0.17 | 0.17 | 0.17 | 0.17 | 0.17 | 0.17 |
Let us focus on node G, whom we shall refer to as "EGO". EGO is connected to 6 people, so each is worth 1/6 of EGO's investment. Now we consider the relationships among these six. Person A is connected to three of EGO's people, so that means that Person A "covers" 3/6 or 50% of EGO's investment. Person B is connected with two of EGO's people, so they "redund with" 2/6 of EGO's alters. The redundancies for all of EGO's alters are given in Table 2:
Table 2. Redundancies in G's Ego Network
| Node "G" is EGO | A | B | C | D | E | F | Total | Eff. Size | Efficiency |
| Redund. with EGO's other Alters: | 3/6 | 2/6 | 0/6 | 1/6 | 1/6 | 1/6 | 1.33 | 4.67 | 77.8% |
Summing the redundancies for each of EGO's alters, we get 1.33. We then subtract 1.33 from the number of alters (6), which gives us 4.67 as the effective size of EGO's network. Had none of EGO's alters been connected with any of the others, the effective size would have been 6. Thus, an effective size of 4.67 represents 77.8% efficiency.
Let us repeat the computation now, taking a different node as EGO. For example, let EGO be node A in Figure 2. EGO has four ties, so each is worth 1/4 (this is what Equation 2 works out). Now we look at each of those four ties to see how many of the other three each is connected to. Person B is connected to just one of EGO's alters (namely, G). Person E is connected to one. Person F is connected to one. And person G is connected to three. Putting this into a table, we get:
Table 3. Redundancies in A's Ego Network
| Node "A" is EGO | G | B | E | F | Total | Eff. Size | Efficiency |
| Redundancy with EGO's other Alters: | 3/4 | 1/4 | 1/4 | 1/4 | 1.50 | 2.50 | 62.5% |
After you calculate total redundancy a few times, you realize that there is a simpler way to think about it. Redundancy is just the average degree of EGO's alters (not counting their tie to EGO). Consider Figure 1 again, with node G as EGO. The within-network degree of each of EGO's alters is {3,2,0,1,1,1}, and the average of these numbers is 1.33, which is what we obtained before. So the effective size of an ego network is just the actual size minus the average degree of the alters.
We can go a little further. The average degree of any network is closely related to its density. In fact it is obvious (2) that the average degree is equal to the density times n-1, where n is the number of nodes in the network. So Burt's redundancy measure is identical to ego network density, scaled by a factor of n-1. This in turn means that a simple formula for the redundancy of any ego network is:
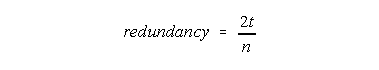
where t is the number of ties in the network (not including ties to ego) and n is the number of nodes (excluding ego). We can then define effective size as:
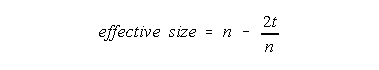
If you're a skeptical reader, you might be tempted to check these shortcuts against the examples in Ron's book. If you did that, you would quickly run into discrepancies. Don't let it shake your confidence: the errors are in the book, not the shortcuts!
For example, on page 53 of Structural Holes, Table 2.1 gives the effective sizes of six networks. One of them is ...
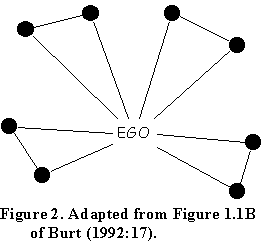
Table 2.1 gives the effective size of this ego network as 4, but this is clearly wrong: the effective size is 7, yielding an efficiency score of 0.875.
Interestingly, the wrong answer has considerable intuitive appeal. Even though there are 8 contacts, there are only 4 separate "pieces" or components of this ego network. A more efficient network would reach 8 separate components with 8 ties. But this is not the way effective size and efficiency were actually defined mathematically.
To see how the effective size measure behaves in practice, I computed it along with a number of other ego network measures on a network of 849 film-makers using the pre-release version of UCINET 5.0 for Windows 95/NT (Borgatti, Everett and Freeman, 1997). The data were compiled by Candy Jones (1993) and consist of who has worked on the same film with whom over a certain period of time. The correlation of Burt's effective size with the other variables is presented here:
| Ego Network Measure | Corr. w/ Burt's Eff. Size |
| Size: | 0.98 |
| No. Of Ties: | 0.95 |
| Density: | -0.58 |
| Avg. Distance:* | 0.56 |
| No. Of Components: | 0.11 |
| Prop. Of Components: | -0.03 |
| Size of 2nd Order Neighborhood: | 0.56 |
| Reach Efficiency: | 0.33 |
*Among connected ego networks
There are several results here that are worth pointing out. First, the correlation with ordinary network size is very high, which suggests that the efficiency rates don't vary a great deal (in this network), and that in practice the humble degree measure can substitute for effective size. Second, you may have expected the correlation with density to be 1.00, since effective size is just n - (n-1)density, which looks like a linear re-scaling. But n (network size) varies from person to person, so across different ego networks the re-scaling is not linear. Third, the correlation with the number of components in the ego network is non-existent, which means that the intuitive notion described above is in fact vastly different from the one that is actually defined.
The measure labeled "size of 2nd order neighborhood" counts the number of distinct nodes within two links of ego (i.e., ego's friends plus ego's friends' friends). The measure labeled "efficiency" is the size of the 2nd order neighborhood divided by the sum of degrees of ego's alters. It is large to the extent that ego's alters connect to different third parties. For a discussion of the logic behind this and related kinds of measures, see Borgatti and Jones (1996).
| Borgatti, S.P., M.G. Everett and L.C. Freeman. 1997. UCINET 5.0. Analytic Technologies. |
| Borgatti, S.P. and C. Jones. 1996. "A Measure of Past Collaboration." Connections 19(1):58-60. |
| Burt, Ronald S. 1995. Structural Holes: The Social Structure of Competition. Harvard University Press, paper back edition. |
| Harary, Frank. 1972. Graph Theory. Addison-Wesley Publishing Company, 3rd printing. |
| Jones, Candace. 1993. Toward a Theory of Network Organization. Ph.D. Dissertation, University of Utah. |
1. Some people believe that mathematical notation is necessarily unambiguous. I don't. It seems to me that mathematical expressions are never fully specified, relying on context and shared knowledge to fill in the missing information.
2. See Harary (1972:14) for a discussion.
| Last revised: 24 January, 2000 | Table of Contents | CONNECTIONS |