Keynote Address

This talk will be a bit unusual it will be a joint talk because we're a team, and have been for almost precisely 25 years. During that time we have written 40-odd papers about a variety of topics in social networks, all stemming from our belief that social networks are amenable to approaches which combine soft and hard science.

By soft science we mean, science conducted on phenomena that don't tend to come with numbers already attached. And by hard science we mean science that has been around long enough to have acquired the ability to have numbers already attached.

That different disciplinary perspectives lead to different questions. That the results of our collaboration are more interesting than either of us could hope to have produced on our own. And that any success we've had comes from respect for each other's discipline -- in sum, that the combination of a naturalist's and a theoretician's skills can be greater than the sum of the two.

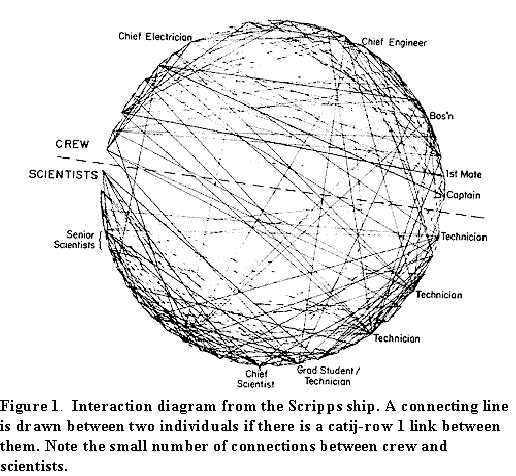
We began our career in social network analysis by gathering data about interactions between individuals. This seemed to us, and still does, to be the basic building block for network knowledge and theory: if there are no interactions there can be no structure. At the time, in 1972, we were both spending a year at the Scripps Institution of Oceanography, just up the street here in San Diego. Russ went to sea with one of the research vessels and wanted to understand something about the social structure: how it formed among a group of people coming on board together, how it developed over time, and so on.

Using a card-sorting task, Russ asked each of the 50-or-so people on the ship to rank order their interactions with all the others. Coming off the ship after several weeks, Russ came to the physics department coffee break (every morning at 10:15 sharp in the venerable Warren Wooster's office) and asked "anybody here want to know the social structure of a vessel that gets all your data?" All of the seasoned ocean-going physicists in the room knew they weren't supposed to talk to people like Russ and didn't even look up.

Not knowing any better, Peter, a theoretical oceanographer, said he thought it might be fun. And that was that.

The card-sorting method was, of course, used widely in cognitive science to study relations among items. We knew that people don't keep a list of sentences in their heads that grammar makes it possible for human beings to learn a finite number of words and produce an infinite number of sentences. Cognitive anthropologists like Kim Romney, Roy D'Andrade, Duane Metzger and Oswald Werner were applying this idea to study how people handled information of all kinds. It was clear that people didn't keep simple lists of animals, foods, illnesses, or kinship terms in their heads. The information about these cultural domains was arranged somehow in people's heads (hierarchically? non- hierarchically? in some kind of dynamic system that we'd now call "hypertext"?) so that people could retrieve it on the fly, as they needed it.

Trained in linguistics and cognitive anthropology in the 1960s, Russ went to sea to apply that logic to the study of social structure: people could not possibly keep in their heads a list of all the people whom they knew much less a list that had all the information attached about their rights and obligations vis-a-vis each person whom they knew.

It was a pretty good idea at least it seemed like a good idea at the time but Russ had no clue about how to make it work. In his field, people who can count above ten without taking off their shoes are called "mathematical anthropologists." (Another definition is an anthropologist who numbers the pages...)

Peter jumped on those data, applied something called the "Baltimore traffic problem algorithm," and Catij one of the family of clique-finders developed in the 1970s was the result. That was a real clue about the importance of a truly cross-disciplinary approach that ideas from totally different fields (in this case, maths applied to solving minimal transit times in traffic) could inform one another.

Catij did a great job, actually. As an ethnographer, Russ naturally took the maps that Catij produced back to the people whom we studied, with me tagging along. The idea was that people could use their own understanding of the social structure to tell us if the mindless algorithm had produced a social structure that made sense, or had produced some senseless artifact. Even discounting the propensity of people to find pattern in, and make sense of, anything [something that would later prove useful in research that challenged our findings about informant accuracy] Catij found some surprising things. In one case, it found a strongly tied pair of people on one of the ships we studied a pair that was not much in touch with the rest of the people on the ship and that, it turned out, were said by others to be, er, a real pair.

I took Catij and applied it to the study of more than a dozen prison living units in two Federal penitentiaries. In the hundreds of groups among the living units we studied, the cliques always made sense. Prison staff would look at the output from Catij and see the patterns: these people in this group here are all whites from big cities in the North; these people are all southern Blacks; these people all committed the same crime. In a memorable case, though, Catij turned up a group of three strongly tied people whose connections made no apparent ethnographic sense: the three had committed different crimes, were mixed North and South, rural and urban, Black and White. The prison staff was stumped. We thought that Catij had finally created an artefact. Until, a week later, the three escaped together.

"No," we told the people at the Federal Bureau of Prisons who had supported the research, Catij was not capable of predicting this sort of thing. But it did make us wonder about whether there might be socially meaningful uses of the sort of thing people were starting to do with social networks in the '70s.

Nonetheless, we -- and especially me, as a hard scientist -- were worried. This was too easy.

You see, for all the success of clique finding algorithms -- CONCOR, ours, and plenty of others -- we were uncomfortable with the results. All the data for these analyses were based on the question: 'who do you talk to?' or some variant thereof ('who do you send memos to in this office?' 'who do you interact with around here?' 'who do you communicate with?' 'who do you ask for advice from?').

Now, let's suppose that informants always tell what they understand to be the truth in response to our questions.

Ignore the fact that even Franz Boas had reminded us generations ago that informants lie. The fact is, informants provide the only source of our data in most cases and we had this uncomfortable feeling that people just do not know too accurately whom they interact with.

What if --oh, dear! -- the level of accuracy among informants was low? Garbage in/garbage out rears its head.

There were two possibilities: either the level wasn't sufficiently high to give us a signal to study, and we were fooling ourselves; or it was.

In the first case, we were dead in the water but we ought to find out. Meanwhile, in the second case when there was a signal to study we must somehow manipulate (smooth) the information we're given in order to get at we hope the underlying truth.

By "truth," of course, we mean the behavior for which informant reports are a proxy. We stipulate that people construct their world. This constructed world is also a "truth." It's just not what we were studying. More on this in a bit.

Data manipulation, especially smoothing to remove noise, is a standard feature of statistics, physics, etc. In those fields, however, we not only know how to do it, we know what we are doing as well, because we understand the underlying physics ("I'm not interested in tides because I'm looking at climate time scales -- hundreds of years -- so I can filter out the daily signals safely").

Catij was based on the presumption that informants have a blurry idea of the structure around them and builds in a particular kind of data smoothing mechanism. As we said, it seemed to work pretty well. But in the study of social networks (social structure) we have no idea what kind of smoothing is necessary because we don't know what kind of noise there is, and we don't know what the underlying physics are either.

We also are painfully aware that most 'theory' for social networks is intrinsically steady-state, whereas most theory for physics posits that 'the rate of change of quantity X is given by the sum of all these things. If X stays constant, then the sum balances to zero' which is a very different way of thinking. At all events, we are stuck with either smoothing -- in a manner we won't understand -- to get data we might be able to build a theory with; or not to smooth, and be stuck with loads of data noise that will probably obscure any advance in understanding.

Here again, we found ourselves asking questions that neither of us would have asked on our own.

Physicists don't often apply their craft to study the structure of social relations. But they should do.

And anthropologists don't often ask whether their data sources are accurate -- or whether that accuracy can be measured. And, of course, they should. Hard scientists, however, ask that question all the time. For example, thanks to orbiting satellites, oceanography from space is big business. But nobody yet has figured out a way to measure the salt content of the ocean (something oceanographers desperately need) from space with any useful accuracy; and so there aren't any instruments flying to measure salt. It's just a waste of time and money.

So we needed to tackle the possibility that there just wasn't a signal to study. We began a study of informant accuracy in social network data. We looked for naturally-occurring groups whose real communication could be unobtrusively monitored and whose members we could ask questions like: "So, in the last [day], [week], [month], who did you talk to in this group?" We began with the deaf people in Washington, DC who had TTYs in their house instead of telephones. When the phone would ring, the lights in their house would flash and they'd know they had a call coming in. They could sit at the teletype and pound away: "Hi, Jane, this is Fred." "Hi, Fred, great to hear from you." This produced a running paper record so the amount of communications between all pairs of people in the study could be measured.

We moved on to monitoring the communications of a ham radio group, embroiling Lee Sailer in all this, and ended up looking at the communications of the infamous Group 35 the social networkers brought together by Linton Freeman to participate in the early experiments by the National Science Foundation of the effects on science productivity of e-mail.

We found the dreaded law that about half of what people tell you is incorrect. Some of the error involves failure to recall behaviors that did occur and some involves recall of behavior that didn't occur.

After a decade of research, we assessed the problem by scouring the literature and putting it in perspective: it turned out the informant-accuracy problem had been recognized many, many times over the years, beginning, as Irv Deutscher reminded us, in 1934 with La Pierre's study of which hoteliers and restaurateurs would, and would not claim to accept Chinese in their establishments. People in nutrition had recognized, in print, that human beings were just awful at recalling accurately the foods they ate. There were plenty of studies on the problem and yet the problem remained a fugitive.

Why wasn't this one of the main issues occupying the efforts of social scientists?

That's the sort of question a naive physicist asks his anthropologist research partner. I mean, it never occurs to the physicist that asking this question might be anything other than an invitation to do some interesting research on an interesting topic.

To our surprise (which we now know to have been naive), our examination of informant accuracy met with immediate and fierce opposition. Some of our colleagues told us privately: "my informants don't lie to me." Well, no, they probably don't, but that uncomfortable feeling we mentioned a minute ago? That was confirmed.

Informants didn't have to lie. They were just terrible at keeping any semblance of an accurate record in their head of whom they talked to yesterday, much less whom they interacted with over the last week or month which is, of course, just the sort of thing they were asked to recall all the time by researchers.

At UC-Irvine, though, Lin and Sue Freeman, Kim Romney, Katie Faust, and Sue Weller re-analyzed our data and reformulated the problem, asking in the process, a very interesting and different question. We had asked: are the instruments for gathering data about human behavior producing valid (accurate) measurements of human behavior? They asked: what do those instruments produce a valid measurement of, anyway? They found that when you ask people about whom they interact with, people tell you whom they think they usually interact with, whom they ought to interact with, given everything they already know about their place in the social structure.

With hindsight, we wonder now, what would be the results of applying the cultural consensus model to our accuracy data?

In any event, we still think that the issue of informant accuracy remains one of the most pressing in the social sciences. Redefining the problem produced very important advances in our understanding of the emics of behavior how emically-defined social structure is created. But it does nothing to advance our understanding of the etics of behavior a topic we think deserves the attention of another generation of researchers.

Now, ignoring the accuracy problem, and supposing the emic description of social structure to be what we're after, all clique finders provide a limited description of that structure. The limitation derives from at least two sources: 1) the particular theory applied in finding subgroups in a set of relations and 2) the particular relations that are represented in the matrix to begin with. That is, if we ask people who in a group they owe money to, we'll get a matrix of debt relations. If we ask people who in the same group they like, we'll get a matrix of affect. There is no expectation that the matrices will be the same and, what's worse, we have no idea which, if either of those matrices is the best, or the right matrix to understand social structure, or even an adequate matrix for understanding a part of the social structure.

Our reasoning was that any matrix of relations might or might not be important, but the rules governing the production of those relations surely must be important. So, taking our cue from the program of research envisioned by Ithiel de Sola Pool and Manfred Kochen in their 1959 article (published after an extraordinary underground career as the first article of the first issue of Social Networks), and from the small world experiments by Stanley Milgram, we asked: what determined who people know? What are the rules governing who people know and how they know each other?

This prompted two lines of research. One followed my normal instinct as a theoretician, the other Russ's as a naturalist. I have to say that the part following my instinct hasn't taken off half as well as the part following Russ's, which must prove something.

Anyway, we got into the business of building simple 'process' models of what the rules might be, with many features obviously of interest suppressed this is how I conduct the rest of my scientific life. We built three models over the next few years: a model of group dynamics (on the individual level); a rather successful pseudo-model of the small world process itself (on the scale of the US population); and a random model of human group evolution (on the scale of world populations).

I don't know what others got out of these models, but we had a hell of a good time.

Peter had the idea of reversing the small world experiment. The small-world experiment told us a few numbers: there are 5.5 links between any two white people in the U.S. and there is exactly one more link between any white and any black person in the U.S. There is no question about how interesting these numbers are. They are the basis of a successful Broadway play and of a wildly popular Internet game (a pop-culture version of calculating Erdös numbers) in which people link film personalities (through a series of films) to Kevin Bacon, a popular current actor.

But these numbers do not tell us anything about the structure of the society. If we showed people a list of small-world targets, complete with the information about targets that Milgram had used (location and occupation), then people could tell us who would be their first link in a small-world experiment. This would give us many repetitions of the experiment for each informant at least the first link and by analyzing the information needed by informants to make their choice of a first link, we could find out something about how the small-world actually operated.

Russ, the ethnographer, wondered: But what if Milgram had guessed wrong? Maybe if people were told the target's religion, then they'd make a different choice of a first link and the chains would all be different? We told a group of 40-some informants about the small-world experiment and then told them the names of 50 targets and nothing else. Informants asked us as many questions as they liked about those 50 targets and we provided the answers (often made up on the spot and, of course, recorded in case another informant asked for the same information). At the end of each of the 50 iterations, the informant told us the name of the first link he or she would choose in a small world experiment to reach each of the 50 targets, and why. That is, the informant told us which piece of information had proved useful in making the decision about that first link.

Christopher McCarty did the interviewing on this experiment. It was a tough experiment to conduct, but we learned several important things. First of all, we learned that experiments requiring interview sessions lasting up to 8 hours were possible if everyone, researchers and informants alike, had enough jelly donuts on hand. 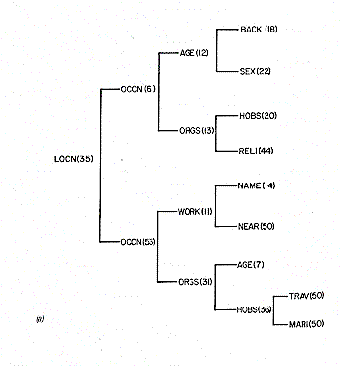And we learned that Milgram was right: despite the fact that informants wanted to know a lot about targets (the targets's hobbies, association memberships, and religion, for example), in the end, location and occupation were mostly what people needed to know about a target in order to make a decision about that first link. (Have a look at Figure 3.)


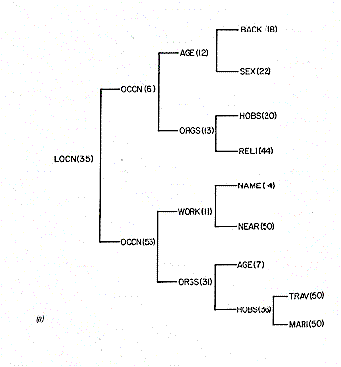Figure 3. Two decision trees from INDEX. The reason for making the choice of question is shown (eg. LOCN means a location question) followed by the percent of time that question was asked in that position of the interview. The following splits follow the decision tree further. (a) trees starting with location of the target; (b) trees starting with sex of the target

This was actually rather important, since by that time we'd already conducted the first of a set of reverse small experiments which cavalierly had assumed that location and occupation were all that people needed to know!

We conducted our first RSW experiment with a list of 1,267 targets, but settled on a final list of 500 100 in each of 4 areas of the world, plus 100 in the country where the experiment was being conducted. In a series of reverse small world experiments using this final instrument, conducted with Paiute Indians and with other cultures in the U.S., as well as in Micronesia and Mexico, we explained the small-world experiment to informants. Then we showed them a list of the 500 names of people from around the world (the people were mythical, but the names were culturally appropriate), complete with location, occupation, hobbies and organizations, and asked informants to name their first link to each target. The things that people in the US find relevant to the task name, location, occupation, hobbies, organizations turn out to be the same as the things people in other cultures need to know to place an alter in their network.

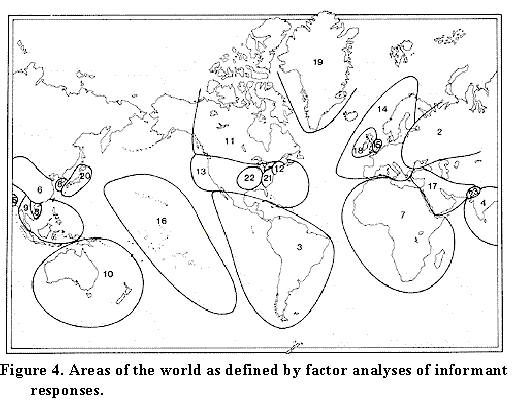
Both of us feel that the cross-cultural regularity discovered in this series of experiments remains for us among the most exciting results of our work. It turned out that informants 'chunked' the world in their heads the same way we did:

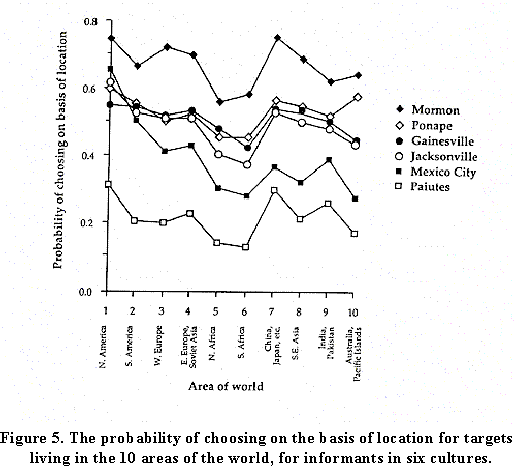
Along the base are -- in no specific order -- 10 areas of the world. The areas are North America; South America; Western Europe, and so on. The y-axis is the probability that informants in the various cultures would pick an intermediary on the basis of the target's location, when the target lived in each of these 10 areas. Remarkably, all the cultures are highly correlated, though with different offsets (Ponape Islanders, for example, have a bias against using location).

So something similar is happening inside people's heads from different cultures.

You can play other games with these data. For example, suppose we create a similarity matrix between targets, based on how many informants select the same choice for a given pair of targets. If this matrix is hit with a multidimensional scaling in two dimensions, and the targets plotted by their location, recognizable, if slightly distorted, maps occur.

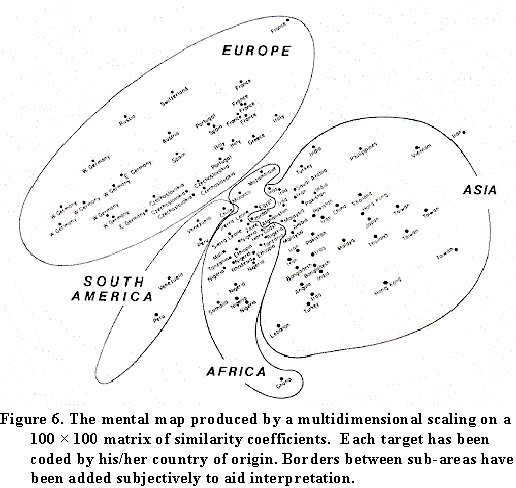
These maps provide convincing evidence of the enduring influence of Gerhard Mercator on the schooling systems of the world!

However, one non-trivial thing did show up. The size of the networks seemed to vary significantly between cultures (and between informants). Why?

Well, all of this work gave us ideas about how the size of networks varied -- but we were working with but one definition of networks (and a specialized one at that). More recently, we extended our interests into what we hope are socially meaningful questions, in particular estimating the size of uncountable sub-populations -- populations like the homeless, and people who are HIV-positive and women who have been raped. In doing this, we've obtained en route much better estimates of how network size varies.

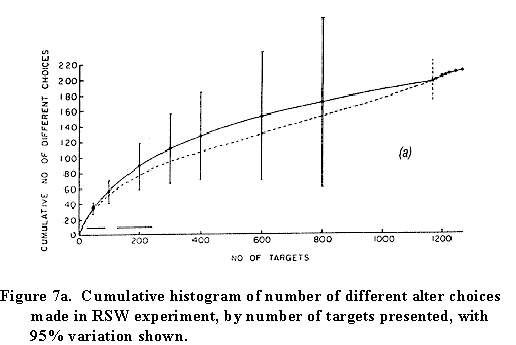
We made a cumulative histogram of the number of network alters generated as each new target on the list was presented. It's clear that with the usual 20/20 hindsight we didn't ask about enough targets.

Our prediction, based on a necessary extrapolation, was that ordinary Americans (represented by the extraordinary citizens of Morgantown, West Virginia who sat through this grueling experiment) would have about 250 people in their networks whom they could call on to be first links if Milgram were to have shown up and asked them to participate in a small world experiment. For estimating the size of the average global network in the U.S., that's a rather specialized definition with which to work, but we had to start somewhere....

Our early estimate was in qualitative agreement with estimates made by Lin Freeman and Claire Thompson, using the phone book method pioneered by Pool (and reported in that classic Pool and Kochen paper). But we only had a point estimate of the average size of social networks. For developing any theory, we'd need to know about the distribution of network size. Nearly 20 years, and some experiments later, we are on a bit more solid ground. 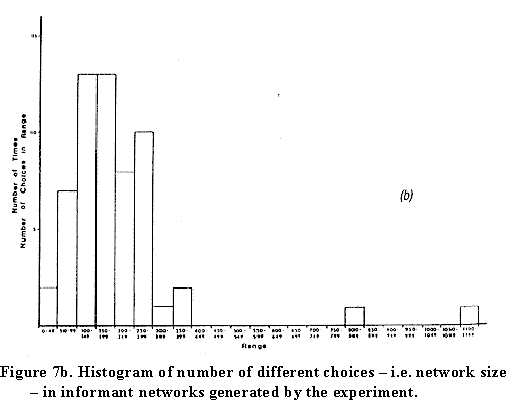Here's a graph showing our current understanding of the distribution of network size for people across the U.S.:

This distribution may be wrong, but as far as we know, this is the only graph showing it. To see how we got it we have to backtrack a little.

October, 1985, just a few weeks after the devastating earthquake in Mexico City. Rubble was everywhere and people had little fishing weights hung by nylon thread from light fixtures in offices across the city. If those little weights went even a couple of degrees out of plumb, people went for the exits and out onto the streets. The government claimed that 6000 people had died, but opposition newspapers and ordinary people everywhere thought that was a macabre joke and that the true figure was perhaps four times the official estimate.

One informant, to make his case, told me: "a lot more than 6,000 died because everyone, but everyone in this city knows someone who died." We could test that, using a very simple model.

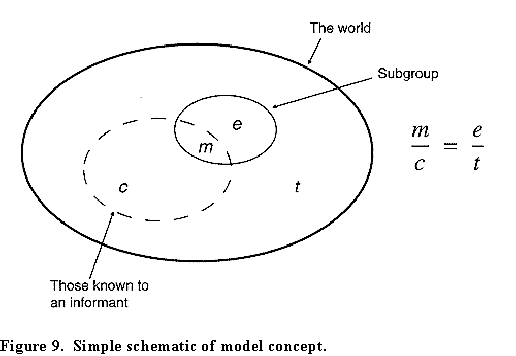
If this simplistic model were true then we could estimate the number of people who had perished in the quake. That is, if everyone knew the same number of people c, and if there were no overlap in who people knew, and we knew the size t of a bigger population in which some uncountable population of interest of size e was embedded and if we could find the probability p that anyone in t knew someone in e, or alternatively how many people m anyone knew in e, then in theory we could solve for e.

Yes, well, if we had some ham, we could have some ham and eggs, if we had some eggs. This model demonstrates clearly that Russ had spent entirely too much of his life around mathmos. He called Gene Johnsen and me. Gene explained that this was a four-part combinatoric with just two knowable pieces: p and t. If we could estimate c, well, then we might get somewhere.

So, with the help of Scott Robinson and his students across Mexico, we ran a street-intercept survey and asked 400 randomly chosen people across Mexico City if they knew someone who had died in the earthquake. Twenty-three percent reported that they did. From this we could deduce what c had to be to give this figure. Later estimates suggested c was around 300. Of course, we had no way to test this, since we didn't know how large c should be for residents of Mexico City.

To make it worse, and most inconsiderately, c isn't a constant. We were able to show how the single number for c was a lower bound on the mean of c across informants, but to improve the estimate for c implied more and better data. We were confident that we could get this by asking informants to tell us whether they knew people in populations whose size we already knew and then working backward.

And so, for the last ten years, working with Gene Johnsen and with two of our ex-students, Gene Ann Shelley and Christopher McCarty we've been developing what we call "network scale-up methods" for estimating the size of populations you can't count.

Our reverse-small world studies had told us that respondents mentally tag their network alters in terms of location and occupation, so in our first test of the model in the Mexico City study we asked people if they knew doctors, mailmen, bus drivers, TV repairmen, and priests (in addition to quake victims).

Estimating a mean c for each sub-population or, more properly, as I said, a lower bound for this quantity gave answers varying by an order of magnitude, with low values based on mailmen and high values based on priests. Inverting this effect, we realized that some populations are simply more visible than others, making reports by respondents biased in one or another direction. Essentially our data suggested that if respondents knew a priest, they were aware of the fact; conversely, they might well know a mailman without being aware of it. We found, in other words, and to our horror, that informants could actually be unaware of information we felt they should know!

In fact, this discrepancy with the simple theory became worse following a survey in Florida based on a different collection of subgroups. We asked people: Do you know any parents of twins? parents of triplets? police officers? surgeons? midwives? These data (which were collected in a survey in Gainesville, Florida by, among others, Tim Brazill) were reported by Gene Johnsen et al., in 1995.

The estimate of the average c for parents of twins was a mere 50, forcing us to accept that knowledge of twins is strongly under-reported or more likely under-known. That is, you can know someone at work or in voluntary associations for years and never find out that he or she has a twin sibling.

Which led us to the not-very-original idea that how information propagates between people is an important part of the glue that ties folk together. To our knowledge, however, the work reported by Gene Shelley (et al., 1990) is original. In that study, Shelley tracked the ordinary things ("his sister had a baby last week") and extraordinary things ("his plane was hijacked last month") that people learn about their network alters across time. Some things take a long time to find out (one of Shelley's informants returned from a college reunion with information about people he hadn't seen in 25 years); some information propagates very quickly.

It would turn out that certain facts about people propagate slowly because people who are defined by those facts have smaller networks. Our initial work on AIDS and HIV-positive populations confirmed this. Using data from the General Social Survey (GSS), Gene Johnsen et al. (1995) found that the estimated network size for AIDS victims was about one-third that for homicide victims. Since there was no a priori reason to suspect this to be the case, we concluded that information that someone has AIDS must spread very selectively in fact, to about one-third the number of people that information about being a homicide victim does.

Gene Shelley's ethnographic interviews with HIV+ persons showed clearly how this worked. The effect of being HIV+ was so stigmatizing and traumatizing, people just pulled back. Yes, they only told certain trusted alters about their HIV status, but their current, active networks were shrinking perhaps toward the number of people who could be trusted to know that HIV status.

We have now identified two types of errors in the propagation of information that affect our estimates of network size and thus, of the size of populations. We call these transmission effects (stigma, for example) and barriers (location, for example) and those effects are the subject of our latest research.

In the last few years we've conducted large-scale surveys to ask a statistically significant group of respondents in detail about many sub-populations (some of known size, some of unknown size), so that we could examine each respondent's knowledge in some detail. One survey was limited to residents of Florida and the other was based on a national, representative sample.

In the Florida survey, we asked respondents about 14 populations based on first names ("do you know someone called Michael?") together with asking how many people were known in other populations of known size (diabetics, licensed pilots, etc.). (The idea of using first names as a set of cues for populations of known sizes was Christopher McCarty's; see McCarty et al., 1997). We also asked about two populations of unknown size, described to telephone respondents as: "someone who is HIV-positive" and "someone who has the disease called AIDS."

That gave us, for each respondent, a pattern of responses, all with the same value of c. One can imagine various methods to deduce a suitable value of c for a particular respondent, and then that value could be used to back-estimate unknown sub-populations.

Our preference is for maximum likelihood methods. The idea is to compute a probability that the responses reported by a respondent could be produced with an individual network of size c(i) (for respondent i). This probability is scanned over all possible values, and the c(i) selected which maximizes that probability.

In the case of subgroups of known size, there is a formula which gives the maximum likelihood estimate of the network size c(i). There is also an estimate of its standard error, which, not surprisingly, becomes more accurate as more (or larger) sub-populations are added, rather like the central limit theorem.

We can then play a similar maximum likelihood game on the populations of unknown size. We have a collection of respondents, each with a "known" c, and all their statements about how many they know in the sub-population of interest. There is thus a size of that sub-population which maximizes the probability of the pattern of reports observed. We also have a standard error of the size as well. Better accuracy is obtained with more people known or, roughly equivalently, simply more respondents.

The Florida survey yielded very promising results. The best estimate of the average c was 108, and the estimated size of the HIV+ population of the U.S. was 1.6 million.

This value for HIV-positive is rather large compared with other estimates, but this survey used only Florida residents, and there is a disproportionately large number of AIDS victims and, we assume, HIV-positive individuals in Florida. If our methods are working, this would bias the result for HIV+ upwards.

We tested all this in the national survey. Based on what we'd learned, and the mistakes we'd made, in the Florida survey, we surveyed 1554 respondents selected to represent the U.S. We asked respondents about 32 sub-populations, including 29 of known size, and three (HIV-positive, rape victims, and homeless) of unknown size.

This method gave an estimate for the average network size c of 286, much larger than the number for Florida respondents and suspiciously like the number we'd found in our first estimate of c in 1978 based on the reverse-small-world experiment.

Here again is the distribution of c. Note the modal value of about 150, with a small number of respondents knowing many people. However, here we've gone back to the two early reverse small world studies and used those data as well (the white circles and the snowflakes).

To be sure, we think they were underestimates (so we increased the values by the relevant ratio); and the binning was different (so we adjusted the frequencies accordingly)...

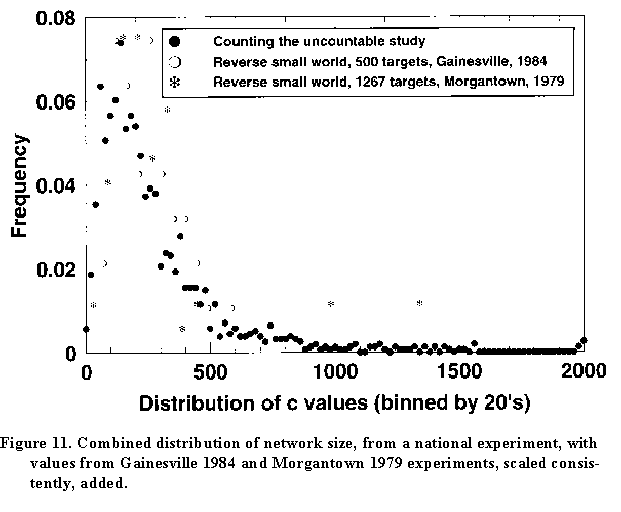
and ... the values overlie rather well. There is something going on out there that is consistent between two totally different experiments. We find that pretty exciting!

The estimate for HIV sero-prevalence is in astonishing agreement with official estimates obtained by much longer and more expensive techniques.

Estimates for homelessness vary strongly; our estimate is much higher than official estimates and much lower than those from advocacy groups, but is very close to the estimate made by the urban institute a decade ago and still widely considered the best estimate available.

Our estimate for the number of rape victims lies in the middle of the range of estimates offered by various colleagues. Any estimate of this population is affected by different definitions of "rape," but our estimate is nearly identical to the one produced by the latest National Crime Victimization Survey.

Social Science has made major achievements. Autism and anorexia are treatable conditions today the result of basic research on stimulus and response in human behavior. That same research, of course, also makes possible the effective marketing of cigarettes to children. The scientific study of management at the beginning of this century produced spectacular gains in productivity and spectacular gains in worker alienation as well. The insurance industry life, medical, home, auto is possible because of fundamental social research and on research about the theory of probabilities. The effective teaching of languages is possible because of sustained, systematic behavioral and cognitive research. Systematic, cross-cultural research has produced a theory of the second demographic transition for the developing world, not just for the industrialized world, with direct and immediate implications for the well-being of billions of people.

We like some of these accomplishments and we don't like others. But all are examples of the serious impact of basic social science research. In the field of social networks, we think the most important task is the discovery of the rules governing who people know and why they know one another.

So, we close with the obligatory assessment of the field and the hortatory rhetoric that everyone expects. In every field of science, there are three broad questions of interest: 1) What is it? That is, what exactly is the nature of the phenomenon in which we are interested? 2) What causes it? and 3) What does it cause? These three questions are answered with description, theory, and prediction. Social network researchers, it seems to us, have done much to answer the first question.

A lot of progress has been made in answering the second as well. From the earliest days of the field, there have been tantalizing indications that structural variables account for at least some of the variance in very important outcome variables: the distribution of resources, including wealth, information, and power; the morbidity of individuals and the probability that they will cope adequately with emotional distress. It seems to us that we now must provide a list of what we think can be predicted from social network variables.

This was also following in P and K's footsteps, and we hope others will follow ours.

Endnotes

1. Keynote speech given at the XVIIth annual Sunbelt International Social Networks Conference. Feb. 13, 1997, San Diego, California. The ordering of authors' names is alphabetical.

The Search for Social Physics(1)

Endnotes

The Search for Social Physics⁽¹⁾