Social network data consists of binary social relations. That is, it records the presence, absence or strength of relationships among pairs of persons. There are many kinds of social relations. For example:
Mathematically, social networks can be represented as graphs or matrices. In this handout we discuss graphs.
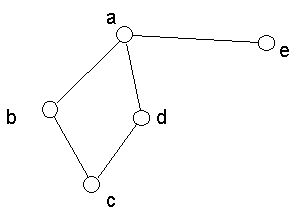
A graph is defined as a set of nodes and a set of lines that connect the nodes. This is sometimes written mathematically as G=(V,E) or G(V,E). Here is one way to draw a graph:
 |
Figure 1. A drawing of a graph. |
It is important to keep in mind that the length of the lines does usually mean anything. This is because all it is representing is that there is or is not a relationship. Similarly, the orientation of the drawing means nothing. For example, node e could have been placed in the middle of the drawing -- this would not mean anything different. The only thing that matters is who is connected to whom.
There are many synonyms for the terms "node" and "line":
| Node | Line |
|---|---|
|
|
The nodes in a graph represent persons (or animals, organizations, cities, countries, etc) and the lines represent relationships among them. The line between persons a and b is represented mathematically like this: (a,b). The network drawn above contains these edges: (a,b), (a,e), (a,d), (b,c), and (d,c).
There are different kinds of graphs. For example, there are directed and undirected graphs. In undirected graphs, the ties have no direction. For example, in Figure 1 above, there is a relationship between a and b, and this is the same thing as saying there is a relationship between b and a. We could refer to the line as (a,b) or (b,a) -- it makes no difference.
In directed graphs (also known as digraphs), the ties do have direction. In such cases, we typically draw the graph with arrowheads, and refer to the lines as "arcs". For example, consider Figure 2. This might record the social relation "who likes whom". Persons b, d and e all say they like person a. Note that person does not say they like d or e, but they do reciprocate with b. Nobody says they like e.
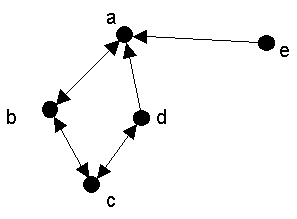 |
Figure 2. A drawing of a directed graph. |
Graphs can also be valued or non-valued. A valued graph has numbers attached to the lines that indicate the strength or frequency or intensity or quantity of the tie between nodes. For example, Figure 3 might record the amount of trade, in trillions of dollars, between some countries:
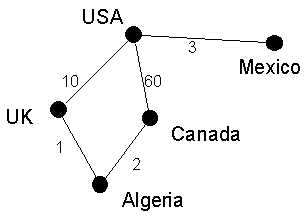 |
Figure 3. Valued graph. |
If a line connects two points, they are said to be "adjacent". The two points connected by a line are called endpoints. An edge that originates or terminates at a given point is "incident" upon that point. Two edges that share a point are also said to be incident.
A subgraph of a graph is a subset of its points together with all the lines connecting members of the subset. The subgraph of Figure 3 that includes the UK, Canada and Algeria has two lines: (UK, Algeria) and (Algeria, Canada).
The degree of a point is defined as the number of lines incident upon that node. In Figure 3, the degree of USA is 3 because it has 3 ties. If a point has degree 0 it is called an isolate. If it has degree 1 it is called a pendant.
In a directed graph, a point has both indegree and outdegree. The outdegree is the number of arcs from that point to other points. In Figure 2, the outdegree of node a is 1. The indegree is the number of arcs coming in to the point from other points. The indegree of node a in Figure 2 is 3.
A path is an alternating sequence of points and lines, beginning at a point and ending at a point, and which does not visit any point more than once. Two (or more) paths are point-disjoint (also known as vertex-independent) if they don't share any nodes. Two paths are edge-disjoint (edge independent) if they don't share any edges. If they are point-disjoint, then they are definitely edge-disjoint. But if they are edge disjoint, they might not be point-disjoint.
A walk is like a path except that there is no restriction on the number of times a point can be visited. A path is a kind of walk.
A cycle is just like a path except that it starts and ends at the same point.
The length of a path or walk (or cycle) is defined as the number of edges in it.
The shortest path between two points is called a geodesic. It is not always unique (that is, there may be several paths between the same two points that are equally short). The graph-theoretic or geodesic distance between two points is defined as the length of the shortest path between them.
[If something is flowing through a network (such as gossip, or a disease), the time that it takes to get from one point to another is partly a function of the graph-theoretic distance between them. Nodes that are not far, on average, from all other nodes, tend to receive what's flowing through the network sooner than other nodes. ]
A graph is connected if there exists a path (of any length) from every node to every other node. The longest possible path between any two points in a connected graph is n-1, where n is the number of nodes in the graph.
A node is reachable from another node if there exists a path of any length from one to the other.
A connected component is a maximal subgraph in which all nodes are reachable from every other. Maximal means that it is the largest possible subgraph: you could not find another node anywhere in the graph such that it could be added to the subgraph and all the nodes in the subgraph would still be connected.
For directed graphs, there strong components and weak components. A strong component is a maximal subgraph in which there is a path from every point to every point following all the arcs in the direction they are pointing. A weak component is a maximal subgraph which would be connected if we ignored the direction of the arcs.
A cutpoint is a vertex whose removal from the graph increases the number of components. That is, it makes some points unreachable from some others. It disconnects the graph.
A cutset is a collection of points whose removal increases the number of components in a graph. A minimum weight cutset consists of the smallest set of points that must be removed to disconnect a graph. The number of points in a minimum weight cutset is called the point connectivity of a graph. If a graph has a cutpoint, the connectivity of the graph is 1. The minimum number of points separating two nonadjacent points s and t is also the maximum number of point-disjoint paths between s and t.
A bridge is an edge whose removal from a graph increases the number of components (disconnects the graph). An edge cutset is a collection of edges whose removal disconnects a graph. A local bridge of degree k is an edge whose removal causes the distance between the endpoints of the edge to be at least k. The edge-connectivity of a graph is the minimum number of lines whose removal would disconnect the graph. The minimum number of edges separating two nonadjacent points s and t is also the maximum number of edge-disjoint paths between s and t.
The centrality of a node in a network is a measure of the structural importance of the node. A person's centrality in a social network affects the opportunities and constraints that they face. There are three important aspects of centrality: degree, closeness, and betweenness.
As defined above, degree centrality is simply the number of nodes that a given node is connected to. If the network consists of who knows whom, degree centrality is the number of people that a given person knows. If the network consists of who has sex with whom, degree centrality is the number of different people that a person has sex with.
In general, the greater a person's degree, the more potential influence they have on the network, and vice-versa. For example, in a gossip network, a person who has more connections can spread information more quickly, and will also be more likely to hear more stuff. This can be both good and bad. In a sexual network, high degree centrality implies a higher risk of disease.
The greater a person's degree, the greater the chance that they will catch whatever is flowing through the network, whether good or bad.
Closeness centrality is defined as the total graph-theoretic distance to all other nodes in the network. For example, in Figure 2 above, node "e" has a closeness score of 8 because it is one link away from "a", two links away from "b" and "d", and three links away from "c". The bigger the number the LESS central they are (because they are farther away from everyone).
When a node has a low closeness score (i.e., is highly central), it tends to receive anything flowing through the network very quickly. This is because the speed with which something spreads in a network is a function of the number of links in the paths traversed. Since nodes with low closeness scores are close to all nodes, they receive things quickly. Once again, whether this is good or bad depends on the situation. In the case of information about what's happening in the company, this is usually good. In the case of a new disease that is spreading, it is very bad to be one of the first people to get it (because doctors have not worked out a treatment yet).
Loosely speaking, betweenness centrality is defined as the number of geodesic paths that pass through a node. It is the number of "times" that any node needs go through a given node to reach any other node by the shortest path.
More precisely, if gij is the number of geodesic paths from i to j and gikj is the number of paths from i to j that pass through k, then gikj/gij is the proportion of geodesic paths from i to j that pass through k. The sum ck = gikj/gij for all i,j pairs is betweenness centrality.
In a diffusion process, a node that has betweenness can control the flow of information, acting as a gatekeeper. This is the classic role played by the executive secretary, who can acquire a great deal of unofficial power this way.
In a network of friendship relations, say, among top players in the personal computer field, the node with high betweennness can serve as a liaison between disparate regions of the network. For example, Bill Gates, head of Microsoft, is part of a certain circle of friends. Larry Ellison, head of Oracle, is part of a different circle of friends. Bill and Larry violently do not get along. Whenever cooperation is needed between Microsoft and Oracle, as in developing standards for network computers, it has to be arranged by a third party that has ties with both camps.
We can think of betweenness as a measure of the extent to which a node is in a position to exploit many structural holes. A structural hole is a gap in a network: a lack of connection between two nodes. A third party that is connected to the two unconnected nodes can sometimes exploit the situation.
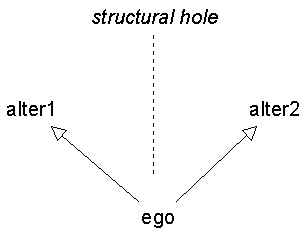
Ego bridges hole between alter1 and alter2
There are two generic benefits to being in the middle. One is the information benefit from being plugged into different camps or regions of the network. If all your ties are to one group of persons who are all interconnected (a "clique"), all you ever hear is the same information being recirculated. The other is the control benefit of being able to play one person against the other. For example, if ego is a woman that alter1 and alter2 are courting, ego can let alter1 know that alter2 is buying her an expensive ring for her birthday. This may lead to alter1 trying to top that with an even better gift.
| Copyright ©1996 Stephen P. Borgatti | Revised: October 08, 1997 | Go to Home page |