Chapter 2 -- Continued
Sociometric Analysis and Graph Theory
The 'gestalt' tradition in psychology, associated principally with the work of K6hler (see K6hler, 1925), involves a stress on the organized patterns through which thoughts and perceptions are
Development of social network analysis 9
structured. These organized patterns are regarded as 'wholes' or systems which have properties distinct from those of their 'parts' and which, furthermore, determine the nature of those parts. The individual objects which people perceive, for example, are seen in the particular way that they are because they are, literally, preconceived within the complex and organized conceptual schemes of the human mind. The ob ects of the world are not perceived independently of these mental schemes but are, in a fundamental sense, constituted by them. Social psychology in this research tradition has stressed the social determination of these conceptual schemes and has, therefore, emphasized the influence of group organization and its associated social climate on individual perceptions.
During the 1930s, many of the leading gestalt theorists fled from Nazi Germany and settled in the United States, where Kurt Lewin, Jacob Moreno (who had migrated to America in 1925) and Fritz Heider became prominent, though rather different, exponents of a gestalt-influenced social psychology. Lewin established a Research Centre at the Massachusetts Institute of Technology, later moving it to Michigan, and this Centre became the focus of research on social perception and group structure. Moreno, on the other hand, explored the possibilities in using psychotherapeutic methods to uncover the structure of friendship choices. Using such techniques as experimentation, controlled observation and questionnaire inquiries, he and his colleagues aimed to explore the ways in which people's group relations served as both limitations and opportunities for their actions and, therefore, for their personal psychological development. Although the word is particularly associated with Moreno, 'sociometric' is an apt description of the general style of research that arose from the gestalt tradition.
Moreno's work was firmly rooted in a therapeutic orientation towards interpersonal relations, reflecting his early medical training and psychiatric practice in Vienna. His aim, elaborated in a major book (Moreno, 1934) and in the founding of a journal (Sociometry, founded in 1937), was to investigate how psychological well-being is related to the structural features of what he termed 'social configurations'. These configurations are formed from the concrete patterns of interpersonal choice, attraction, repulsion, friendship and other relations in which people were involved, and they are the basis upon which large-scale 'social aggregates', such as the economy and the state, are sustained and reproduced over time. Moreno's concern for the relationship between small-scale interpersonal configurations and large-scale social aggregates is a very clear expression of some of the leading ideas of classical German sociology, most notably those developed in the works of Weber,
10 Social network analysis
Toennies and Simmel. Indeed, the latter's 'formal sociology' is a direct precursor of many sociometric concerns (Simmel, 1908; Aron, 1964).
Moreno's chief innovation was to devise the 'sociogram' as a way of representing the formal properties of social configurations. The latter could be represented in diagrams analogous to those of spatial geometry, with individuals represented by 'points' and their social relationships to one another by 'lines'. This idea is now so well established and taken for granted that its novelty in the 1930s is difficult to appreciate. Before Moreno, people had spoken of 'webs' of connection, the 'social fabric' and, on occasion, of 'networks' of relations, but no one had attempted to systematize this metaphor into an analytical diagram.
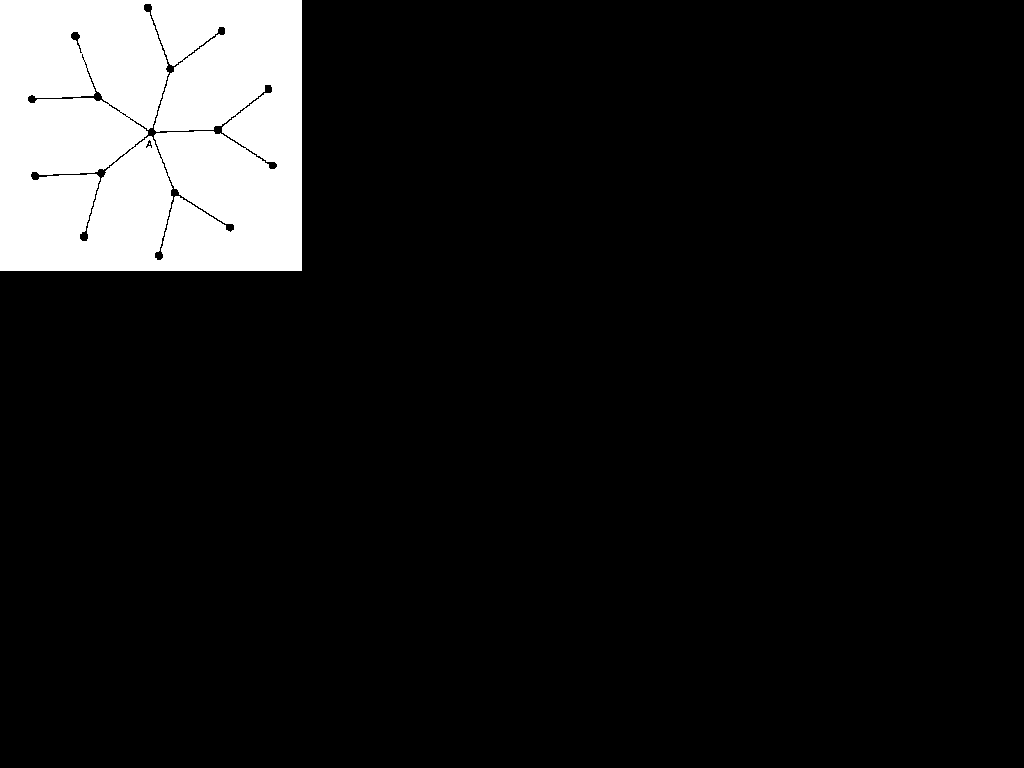
For Moreno, social configurations had definite and discernible structures, and the mapping of these structures into a sociogram allowed a researcher to visualize the channels through which, for example, information could flow from one person to another and through which one individual could influence another. Moreno argued that the construction of sociograms allowed researchers to identify leaders and isolated individuals, to uncover asymmetry and reciprocity, and to map chains of connection. One of his principal sociometric concepts was that of the sociometric 'star', the recipient of numerous and frequent choices from others and who, therefore, held a position of great popularity and leadership. For Moreno, the concept of the 'star' pointed to an easily visualized picture of the relations among group members. In Figure 2.2, for example, person A is the recipient of friendship choices from all the other members of a group, yet A gives reciprocal friendship choices only to persons B and C. A is, therefore, the star of attraction within the group.
Lewin's early work on group behaviour was published in a book which outlined his view that group behaviour was to be seen as determined by the field of social forces in which the group was located (Lewin, 1936). A social group, he argued, exists in a 'field', a social 'space' which comprises the group together with its surrounding environment. But the environment of the group is not seen as something purely external to and independent of the group. The environment that really matters to group members is the perceived environment. The perceived environment is what writers in the symbolic interactionist tradition called the 'definition of the situation', and its social meaning is actively constructed by grcup members on the basis of their perceptions and experiences of the contexts in which they act. The group and its environment are, therefore, elements within a single field of relations. The structural properties of this social space, Lewin argued, can be analysed
Development of social network analysis 1 1

Figure 2.2 A sociogram: the sociometric star
through the mathematical techniques of topology and set theory (Lewin, 1951). The aim of 'field theory' is to explore, in mathematical terms, the interdependence between group and environment in a system of relations, a view which brought Lewin close to subsequent developments in general systems theory. (See Buckley, 1967 for an application of this framework to sociology.)
In a topological approach, the social field is seen as comprising 'points' connected by 'paths'. The points represent individual persons, their goals, or their actions, and the paths represent the interactional or causal sequences which connect them. The field model, therefore, describes causal and interactional interdependencies in social configurations. The paths which run between points tie them together, and the pattern of paths divides a field into a number of discrete 'regions'. Each region is separated from the others by the absence of paths between them: paths run within but not between the regions. The opportunities which individuals have to move about in their social world are determined by the boundaries between the different regions of the field in which they are located. The constraints imposed by these boundaries are the 'forces' which determine group behaviour. The total social field, therefore, is a field of forces acting on group members and shaping their actions and experiences.
A further strand of cognitive psychology which made a major contribution to the development of theories of group dynamics was the work of Heider. His initial work was on the social psychology of attitudes and perception, and Heider was especially concerned with how a person's various attitudes towards others are brought into a state of 'balance'. The different attitudes which an individual holds
12 Social network analysis
are balanced in his or her mind when they do not produce a state of psychological tension. Psychological balance, therefore, depends on the holding of attitudes which are not contradictory with one another. Heider's particular concern was with interpersonal balance, the congruence (or lack of congruence) among attitudes to other people. He was concerned, for example, with how a person who is emotionally close to two other people might respond to any perceived conflict or hostility between them. In such a situation, there is an imbalance in the whole field of attitudes. Heider (1946) held that attitudes can be seen, at their simplest, as positive or negative. 'Balance' exists among a set of attitudes when they are similar to one another in their sign - all positive or all negative. If person A likes person B, and person B likes person C, a state of balance exists only if A also likes C. All the attitudes are 'positive'. It is important to note that, for Heider as for Lewin, this kind of analysis relates to the way in which the world is perceived from the standpoint of a focal individual: Heider was adopting an explicitly ,phenomenological' stance. From this point of view, the important thing is not the actual relation between B and C, but A's perception (accurate or otherwise) of this relationship. 'Balance' refers to a psychological, phenomenological state, and not to any actually existing relations in a social group.
While field theory, as a theoretical framework for social analysis, proved a dead-end, Lewin's advocacy of mathematical models of group relations proved to be a fruitful foundation for later work. Of particular importance in building on the insights of Lewin was Cartwright, who, together with the mathematician Harary, pioneered the application of graph theory to group behaviour (Cartwright and Zander, 1953; Harary and Norman, 1953; see also Bavelas, 1950). Graph theory had first been formulated by K6nig in 1936, but, like many works published in Germany in the 1930s, it had little immediate impact on the wider intellectual world. Its significance for the mainstream of intellectual effort was appreciated only in 1950, when his book (Kbnig, 1936) was republished in the United States and its ideas were developed in the work of Harary and Norman (1953). These mathematical ideas made possible a crucial breakthrough in the theory of group dynamics. This breakthrough consisted of moving from the concept of cognitive balance in individual minds to that of interpersonal balance in groups. Newcomb (1953) was one of the first researchers to move in this direction, arguing that there was a tendency for two people who were close to one another to adopt similar attitudes towards third parties or events. Researchers could, therefore, build models of the systematic interdependence between the attitudes held by
Development of social network analysiv 13
different individuals within a group. This claim was generalized within the theoretical framework outlined by Cartwright and Harary (1956). In the hands of these writers, the insights of Lewin, Moreno and Heider were brought together into a novel and more powerful synthesis (see also Harary, Norman and Cartwright, 1965, which was under preparation from the mid-1950s). The attempt to apply mathematics to the structure of group relations was not, of course, a new idea - as well as the work of Lewin there were other early contributions, using different mathematical models, at the end of the 1940s (for example, Bavelas, 1948 and Festinger, 1949). Building on Lewin's work, however, Cartwright, Zander and Harary evolved powerful models of group cohesion, social pressure, cooperation, power and leadership.
Cartwright and Harary (1956) had outlined the basic idea of representing groups as collections of points connected by lines - the basic insight of Moreno. The resulting sociogram or 'graph' represented the network of actual interpersonal relations among group members and could be analysed, they argued, by using the mathematical ideas of graph theory. Graph theory has nothing to do with the graphs of variables familiar from school mathematics. Instead, a graph is simply a set of lines connecting points, and graph theory consists of a body of mathematical axioms and formulae which describe the properties of the patterns formed by the lines. In the work of Cartwright and Harary, the points in a graph represented individuals and the lines showed their relations with one another. The lines in a graph can be given signs (+ or -) to indicate whether they refer to 'positive' or 'negative' relations, and they can be given arrow heads to indicate the 'direction' of the relationships. The direction attached to a line is a way of distinguishing, for example, person A's orientation to person B from B's orientation to A: person A may direct a positive relation to B (he likes B), while person B may direct a negative relation to A (she hates A). This construction of 'signed' and 'directed' graphs allowed Cartwright and Harary to analyse group structure from the standpoint of each of its members simultaneously, and not simply from the standpoint of a particular focal individual. It was, therefore, a major move forward in a strictly sociological direction.
The fundamental points that Cartwright and Harary were making can most easily be understood by considering the case of 'undirected' graphs. In an undirected graph, the relation of A to B is assumed to be identical with the relation of B to A. This can occur, for example, because their attitudes are perfectly reciprocated or because they have a common involvement in the same activity. For this reason, the line between any two points can be studied without considering
14 Social network analysis
its direction. In an undirected graph, 'balance' describes simply the particular patterns of signs attached to the lines which make up the graph. In Figure 2.3, for example, three different graphs of relations

Figure 2.3 Balanced and unbalanced structures
among three actors are shown. In graph (i), A and B have a positive relationship to one another and the whole graph is balanced because of the existence of positive relations between A and C and between B and C. In graph (ii), however, a negative relation between A and C puts a strain on the positive relation between A and B, because of the positive relation which exists between B and C: the graph is unbalanced. Put simply, if my friend likes someone to whom I am antagonistic, there is likely to be a strain in the relation between us. I might be expected to respond to this by persuading my friend to give up their liking of the third party, by altering my own relation to that person, or by breaking the relationship with my friend. Each participant in an unbalanced network will be under a similar strain and so will be attempting to resolve the tensions that they experience.' Group relations are in a dynamic flux, with the final balanced outcome - if it is achieved - resulting from the actions and compromises of all the participants involved. Responses aimed at restoring balance to the group can be mapped in new graphs with
Development of social network analysis 15
different signs attached to the various lines. Graph (iii), for example, represents the situation where A successfully persuades B to dislike C and so restores balance.
Cartwright and Harary argued that complex social structures can be seen as built from simple structures. More particularly, they are composed of overlapping 'triads' such as those depicted in Figure 2.3. Simple triadic structures are the building blocks of larger social structures, and the properties of complex networks of social relations can, they argue, be derived from an analysis of these building blocks. In the simplest case, for example, a whole network is balanced when all of its constituent triads are balanced. While the idea of a balanced triad is, perhaps, fairly clear and comprehensible, the idea that a large and complex network is 'balanced' is less so. Indeed, the claim might seem to be neither an interesting nor a useful piece of information. This would, however, be an erroneous conclusion to draw. A very important finding, which has been derived from the work of Cartwright and Harary, is that any balanced graph, no matter how large or complex, can be divided into two sub-groups with rather interesting properties: the relations within each of these sub-groups will be positive, while those between the sub-groups will be negative. Thus, a balanced social network, defined, for example, by relations of solidarity, will consist of two cohesive sub-groupings between which there is conflict and antagonism.
In the simple case where all the relations in a network are positive, one of these sub-groups will be an empty or null set: all points will fall into a single group. 3 This will not be the case in more complex balanced structures, and a division into subgroups might highlight important structural features of the network. So, the identification of a network as balanced or unbalanced is merely a first step in the move towards its 'decomposition' into its constituent sub-groups. Much of the mathematical work concerned with the analysis of balance has centred on the attempt to discover such decomposition techniques. The successful decomposition of a balanced network would allow researchers to derive an understanding of network structure simply from information about the relations between individuals. This discovery has enormous implications for the understanding of group structure, and James Davis (1967, 1968) has been a leading figure in the attempt to discover the conditions under which it might be possible to move towards more realistic decomposition techniques which would allow researchers to identify the existence of more than two sub-groups within a network.'
The notion of balance has been especially influential in experimental studies of group cooperation and leadership and has resulted
16 Social network analysis
in one classic study of small group behaviour in a natural setting (Festinger et al., 1959). Many of the ideas which emerged from the sociometric tradition of small group research were, however, taken up by researchers with an interest in general systems theory and in the mathematical aspects of cybernetics and rational action. Indeed, the first applications of sociometric ideas to large-scale social systems were initiated by just such researchers. Initial studies explored the spread of disease from one person to another through chains of contacts, aiming at the derivation of predictive epidemiological models of contagion. A leading figure in this work was Rapoport, who elaborated on the formal implications of the studies (Rapoport, 1952, 1958) and helped to stimulate an interest in applying similar ideas to the transmission of ideas and innovations. Although such work has been undertaken before, along with investigations of the spread of rumour and gossip, the 1960s saw the first major works of this kind to use network concepts (Fararo and Sunshine, 1964; Coleman et al., 1966).
Return to Table of Contents