The idea of the centrality of individuals and organizations in their social networks was one of the earliest to be pursued by social network analysts. The immediate origins of this idea are to be found in the sociometric concept of the 'star' - that person who is the most 'popular' in his or her group or who stands at the centre of attention. The formal properties of centrality were initially investigated by Bavelas (1950), and, since his pioneering work, a number of competing concepts of centrality have been proposed. As a result of this proliferation of formal measures of centrality, there is considerable confusion in the area. What unites the majority of the approaches to centrality is a concern for the relative centrality of the various points in the graph the question of so-called 'point centrality'. But from this common concern they diverge sharply. In this chapter I will review a number of measures of point centrality, focusing on the important distinction between 'local' and 'global' point centrality. A point is locally central if it has a large number of connections with the other points in its immediate environment if, for example, it has a large 'neighbourhood' of direct contacts. A point is globally central, on the other hand, when it has a position of strategic significance in the overall structure of the network. Local centrality is concerned with the relative prominence of a focal point in its neighbourhood, while global centrality concerns prominence within the whole network.
Related to the measurement of point centrality is the idea of the overall 'centralization' of a graph, and these two ideas have sometimes been confused by the use of the same term to describe them both. Freeman's important and influential study (1979), for example, talks of both 'point centrality' and 'graph centrality'. Confusion is most likely to be avoided if the term ;centrality' is restricted to the idea of point centrality, while the term 'centralization' is used to refer to particular properties of the graph structue as a whole. Centralization, therefore, refers not to the relative prominence of points, but to the overall cohesion or integration of the graph. Graphs may, for example, be more or less centralized around particular points or sets of points. A number of different
86 Social network analysis
procedures have been suggested for the measurement of centralization, contributing further to the confusion which besets this area. Implicit in the idea of centralization is that of the structural 'centre' of the graph, the point or set of points around which a centralized graph is organized. There have been relatively few attempts to define the idea of the structural centre of a graph, and it will be necessary to give some consideration to this.
The concept of point centrality, I have argued, originated in the sociometric concept of the 'star'. A central point was one which was 'at the centre' of a number of connections, a point with a great many direct contacts with other points. The simplest and most straightforward way to measure point centrality, therefore, is by the degrees of the various points in the graph. Tle degree, it will be recalled, is simply the number of other points to which a point is adjacent. A point is central, then, if it has a high degree; the corresponding agent is central in the sense of being 'well-connected' or 'in the thick of things'. A degree-based measure of point centrality, therefore, corresponds to the intuitive notion of how well connected a point is within its local environment. Because this is calculated simply in terms of the number of points to which a particular point is adjacent, ignoring any indirect connections it may have, the degree can be regarded as a measure of local centrality. The most systematic elaboration of this concept is to be found in Nieminen (1974). Degree-based measures of local centrality can also be computed for points in directed graphs, though in these situations each point will have two measures of its local centrality, one corresponding to its indegree and the other to its outdegree. In directed graphs, then, it makes sense to distinguish between the 'in-centrality' and the 'out-centrality' of the various points.
A degree-based measure of point centrality can be extended beyond direct connections to those at various path distances. In this case, the relevant 'neighbourhood' is widened to include the more distant connections of the points. A point may, then, he assessed for its local centrality in terms of both direct (distance 1) and distance 2 connections or, indeed, whatever cut-off path distance is chosen. The principal problem with extending this measure of point centrality beyond distance 2 connections is that, in graphs with even a very modest density, the majority of the points tend to be linked through indirect connections at relatively short path distances. Thus, comparisons of local centrality wares at distance 4, for example, are
Centrality and centalizalion 87
unlikely to be informative if most of the points are connected to most other points at this distance. Clearly, the cutoff threshold which is to be used is a matter for the informed judgment of the
researcher who is undertaking the investigation, but distance 1 and distance 2 connections are likely to be the most informative in the majority of studies.

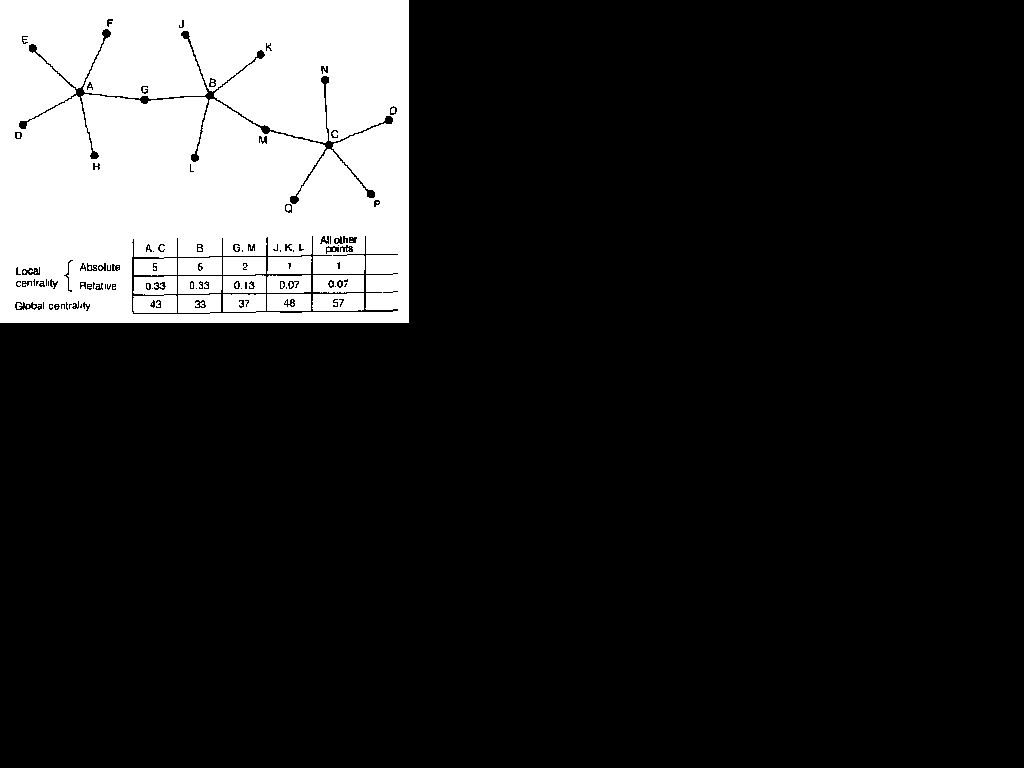
Figure 5.1 Local and global centrality
It is important to recognize that the measurement of local centrality does not involve the idea that there will be any unique ,central' point in the network. In Figure 5. 1, for example, points A, B and C can each be seen as local centres: they each have a degree of 5 , compared with degrees of I or 2 for all other points. Even if point A had many More direct connections than points B and C it would not be 'the' centre of the network: it lies physically towards one 'side' of the chain of points, and its centrality is a purely 'local' phenomenon. The degree, therefore, is a measure of local centrality, and a comparison of the degrees of the various points in a graph can show how well connected the points are with their local environments.
This measure of local centrality has, however, one major limitation. This is that comparisons of centrality mores can only
98 Social network analysis
meaningfully be made among the members of the same graph or between graphs which are the same size. The degree of a point depends on, among other things, the size of the graph, and so measures of local centrality cannot be compared when graphs differ significantly in size. The use of the raw degree score may, therefore, be misleading. A central point with a degree of 25 in a graph of 100 points, for example, is not as central as one with a degree of 25 in a graph of 30 points, and neither can be easily compared with a central point with a degree of 6 in a graph of 10 points, In an attempt to overcome this problem, Freeman (1979) has proposed a relative measure of local centrality in which the actual number of connections is related to the maximum number which it could sustain. A degree of 25 in a graph of 100 points, therefore, indicates a relative local centrality of 0.25, while a degree of 25 in a graph of 30 points indicates a relative centrality of 0,86, and a degree of 6 in a graph of 10 points indicates a relative centrality of 0.66.' Figure 5.1 shows that relative centrality can also t-e used to compare points within the same network, It should also be clear that this idea can be extended to directed graphs. A relative measure, therefore, gives a far more standardized approach to the measurement of local centrality.
The problem of comparison which arises with raw degree measures of centrality is related to the problem of comparing densities between different graphs, which was discussed in the previous chapter. Both are limited by the question of the size of the graphs. It will be recalled, however, that the density level also depends on the type of relation that is being analysed. The density of an 'awareness' network, I suggested, would be higher than that of a 'loving' network. Because both density and point centrality are computed from degree measures, exactly the same considerations apply to measures of point centrality. Centrality measured in a loving network, for example, is likely to be lower, other things being equal, than centrality in an awareness network. Relative measures of point centrality do nothing to help with this problem. Even if local centrality scores are calculated in Freeman's relative terms, they should be compared only for networks which involve similar types of relations.
Local centrality is, however, only one conceptualization of point centrality, and Freeman (1979, 1990) has proposed a measure of global centrality based around what he terms the 'closeness' of the points. Local centrality measures, whatever path distance is used, are expressed in terms of the number or proportion of points to which a point is connected. Freeman's measure of global centrality is expressed in terms of the distances among the various points. it
Centrality and centalization 89
will be recalled that two points are connected by a path if there is a .sequence of distinct lines connecting them, and the length of a path is measured by the number of lines which make it up. In graph theory, the length of the shortest path between two points is a measure of the distance between them. The shortest distance between two points on the surface of the earth lies along the geodesic which connects them, and, by analogy, the shortest path between any particular pair of points in a graph is termed a `geodesic'. A point is globally central if it lies at short distances from many other points. Such a point is 'close' to many of the other points in the graph.
The simplest notion of closeness is, perhaps, that calculated from the 'sum distance', the sum of the geodesic distances to all other points in the graph (Sabidussi, 1966). If the matrix of distances between points in an undirected graph is calculated, the sum distance of a point is its column or row sum in this matrix (the two values are the same). A point with a low sum distance is 'close' to a large number of other points, and so closeness can be seen as the reciprocal of the sum distance. In a directed graph, of course, paths must be measured through lines which run in the same direction, and, for this reason, calculations based on row and column sums will differ. Global centrality in a directed graph, then, can be seen in terms of what might be termed 'in-closeness' and 'out-closeness'.
The table in Figure 5.1 compares a sum distance measure of global centrality with degree-based measures of absolute and relative local centrality. It can be seen that A, B and C are equally central in local terms, but that B is more globally central than either A or C. In global terms, G and M are less central than B, but more central than the locally central points A and C. These distinctions made on the basis of the sum distances measure, therefore, confirm the impression gained from a visual inspection of the graph. This is also apparent in the measures for the less central points. All the remaining points have a degree of 1, indicating low local centrality, yet the sum distance measure clearly brings out the fact that J, K and L are more central in global terms than are the other points with degree 1.
Freeman (1979) adds yet a further concept of point centrality, which he terms the betweenness. This concept measures the extent to which a particular point lies 'between' the various other points in the graph: a point of relatively low degree may play an important 'intermediary' role and so be very central to the network. Points G and M in Figure 5. 1, for example, lie between a great many pairs of points. The betweenness of a point measures the extent to which an agent can play the pan of a 'broker' or 'gatekeeper' with a potential
90 Social network analysis
for control over others. G could, therefore, be interpreted as an intermediary between the act of agents centred around B and that centred around A, while M might play the same role for the sets of B and C.
Freeman's approach to betweenness is built around the concept of 'local dependency'. A point is dependent upon another if the paths which connect it to the other points pass through this point. In Figure 5. 1, for example, point E is dependent on point A for access to all other parts of the graph, and it is also dependent, though to a lesser extent, on points G, B, M and C.
Betweenness is, perhaps, the most complex of the measures of point centrality to calculate. The 'betweenness proportion' of a point Y for a particular pair of points X and Z is defined as the proportion of geodesics connecting that pair which pass through Y it measures the extent to which Y is 'between' X and Z 3 'Me 'pair dependency' score of point X on point Y is then defined as the sum of the betweenness proportions of Y for all pairs which involve X. The 'local dependency matrix' contains these pair dependency scores, the entries in the matrix showing the dependence of each row element on each column element. The overall 'betweenness' of a point is calculated as half the sum of the values in the columns of this matrix, i.e., half the sum of all pair dependency scores for the points represented by the columns. Despite this rather complex calculation, the measure is intuitively meaningful, and it is easily computed with the UCINET and GRADAP programs.
In Freeman's work, then, can be found the basis for a whole family of point centrality measures: local centrality (degree), betweenness and global centrality (closeness), I have shown how comparability between different social networks can be furthered by calculating local centrality in relative rather than absolute terms, and Freeman has made similar proposals for his other measures of centrality. He has produced his own relative measure of betweenness, and he has used a formula of Beauchamp (1965) for a relative closeness measure. All these measures, however, are based on raw scores of degree and distance, and it is necessary to turn to Bonacich (1972, 1987) for an alternative approach which uses weighted scores.
Bonacich holds that the centrality of a particular point cannot be assessed in isolation from the centrality of all the other points to which it is connected. A point which is connected to central points has its own centrality boosted, and this, in turn, boosts the centrality of the other points to which it is connected (Bonacich, 1972). There is, therefore, an inherent Circularity involved in the calculation of
Centrality and centralization 91
centrality. According to Bonacich, the local centrality of point i in a graph, ci, is calculated by the formula rijcj, where rij is the value of the line connecting point i and point i and cj is the centrality of point j. That is to say, the centrality of i equals the sum of its connections to other points, weighted by the centrality of each of these other points.
Bonacich (1987) has subsequently generalized his initial approach, did Freeman. to a whole family of local and global measures. The most general formula for centrality, he argued, is ci = rijcj ( + cj). In this formula, the centrality weighting is itself modified by the two parameters , and . is introduced simply as an arbitrary standardizing constant which ensures that the final centrality measures will vary around a mean value of 1. , on the other hand, is of more substantive significance, It is a positive or negative value which allows the researcher to set the path distances which are to be used in the calculation of centrality. Where is set as equal to zero, no indirect links are taken into account, and the measure of centrality is a simple degree-based measure of local centrality. Higher levels of increase the path length, so allowing the calculation to take account of progressively more distant connections. Bonacich claims that measures based on positive values of correlate highly with Freeman's measure of closeness.
A major difficulty with Bonacich's argument, however, is that the values given to 0 are the results of arbitrary choices made by researchers. It is difficult to know what theoretical reasons there might be for using one 0 level rather than another. While the original Bonacich measure may be intuitively comprehensible, the generalized model is more difficult to interpret for values of P which are greater than zero. On the other hand, the suggestion that the value of 0 can be either positive or negative does provide a way forward for the analysis of signed graphs. Bonacich himself suggests that negative values correspond to 'zero-sum' relations, such as these involved in the holding of money and other financial resources. Positive values, on the other hand, correspond to 'non-zero-sum' relations, such as those involving access to information.
I have discussed centrality principally in terms of the most central points in a graph, but it should be clear that centrality scores also allow the least central points to be identified. Those points with the lowest centrality, however this is measured, can be regarded as the peripheral points of the graph. This is true, for example, for all the points in Figure 5.1 which have degree 1. They are locally peripheral in so far as they are loosely connected into the network. The global centrality scores in Figure 5.1, however, show that points J,
92 Social netwok analysis
K and L are not as globally peripheral as the other points with degree 1.
Centralization and Graph Centres
I have concentrated, so far, on the question of the centrality of particular points. But it is also possible to examine the extent to which a whole graph has a centralized structure. The concepts of density and centralization refer to differing aspects of the overall 'compactness' of a graph. Density describes the general level of cohesion in a graph; centralization describes the extent to which this cohesion is organized around particular focal points. Centralization and density, therefore, are important complementary measures.
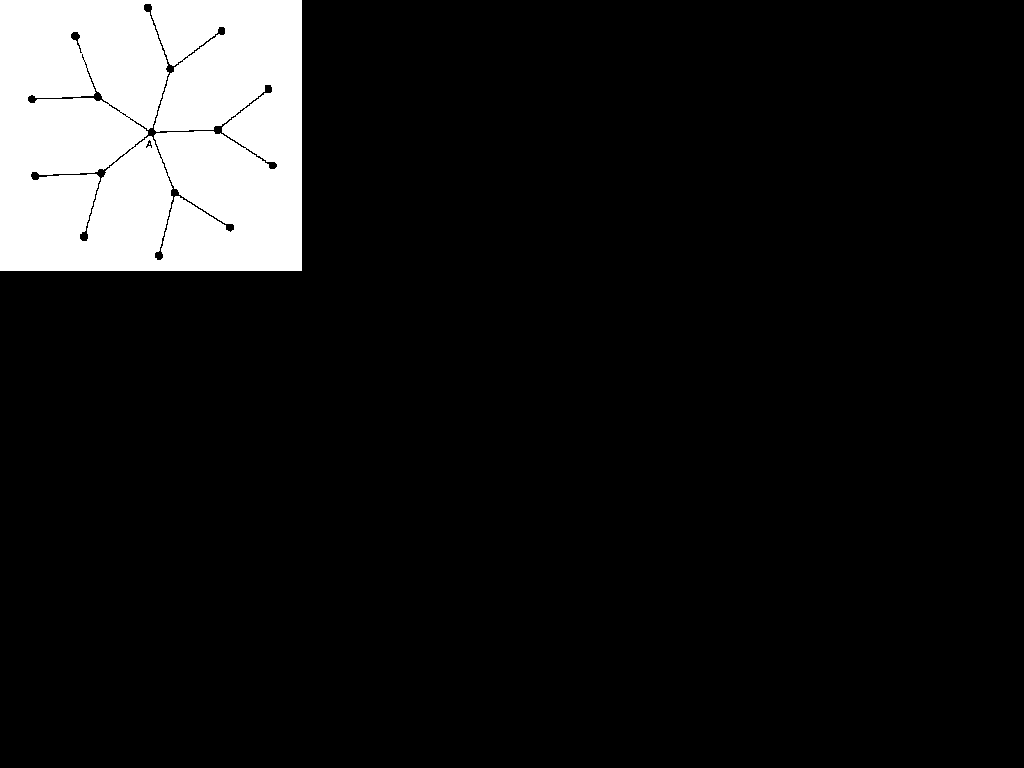
Figure 5.2 A highly centralized graph
Figure 5.2 shows a simplified model of a highly centralized graph: the whole graph is organized, in important respects, around point A as its focal point, How is this level of centralization to be measured? Freeman (1979) has shown how measures of point centrality can be converted into measures of the overall level of centralization which is found in different graphs. A graph centralization measure is an expression of how tightly the graph is organized around its most central point. Freeman's measures of centralization are attempts to isolate the various aspects of the simplified notion of centralization. On this basis, he identifies three types of graph centralization,
Centrality and centralization 93
rooted in the varying conceptions of point centrality which Freeman has defined.
The general procedure involved in any measure of graph centralization is to look at the differences between the centrality scores of the most central point and those of all other points. Centralization, then, is the ratio of the actual sum of differences to the maximum possible sum of differences. The three different ways of operationalizing this general measure which Freeman discusses follow from the use of one or other of the three concepts of point centrality. Freeman (1979) shows that all three measures vary from 0 to I and that a value of I is achieved on all three measures for graphs structured in the form of a 'star' or 'wheel'. He further shows that a value of 0 is obtained on all three measures for a 'complete' graph. Between these two extremes lie the majority of graphs for real social networks, and it is in these cases that the choice of one or other of the measures will be important in illuminating specific structural features of the graphs. A degree-based measure of graph centralization, for example, seems to be particularly sensitive to the local dominance of points, while a betweenness-based measure is rather more sensitive to the 'chaining' of points.
Assessing the centralization of a graph around a particular focal point is the starting point for a broader understanding of centralization. Measures of centralization can tell us whether a graph is organized around its most central points, but they do not tell us whether these central points comprise a distinct set of points which cluster together in a particular part of the graph. The points in the graph which are individually most central, for example, may be spread widely through the graph, and in such cases a measure of centralization might not be especially informative. It is necessary, therefore, to investigate whether there is an identifiable 'structural centre' to a graph. The structural centre of a graph is a single point or a cluster of points which, like the centre of a circle or a sphere, is the pivot of its organization,
This approach to what might be called 'nuclear centralization' has been outlined in an unpublished work of Stokman and Snijders,,' Their approach is to define the set of points with the highest point centrality scores as the 'centre' of the graph. Having identified this set, researchers can then examine the structure of the relations between this set of points and all other points in the graph. A schematic outline of the Stokman and Snijders approach is shown in Figure 5.3.
If all the points in a graph are listed in order of their point centrality - Stokman and Snijders use local centrality then the set
94 Social netwok analysis

Figure 5.3 The I .. t,,al ... to, of , graph
of points with the highest centrality is the centre. The boundary between the centre and the rest of the graph is drawn wherever there appears to be a 'natural break' in the distribution of centrality scores. The decrease in the centrality score of each successive point may, for example, show a sharp jump at a particular point in the distribution, and this is regarded as the boundary between the centre and its 'margin'. The margin is the set of points hich clusters close to the centre and which is, in turn, divided from the 'peripheral' points by a further break in the distribution of centrality scores.
The Stokman and Snijders concept applies only to highly centralized graphs. In a graph such as that in Figure 5.2, which is centralized around a particular set of central points, as measured by one of Freeman's indicators. it may be cry informative to try to identify the sets defined by Stokman and Snijders, though there ill be an inevitable arbitrariness in identifying the boundaries between centre, margin and periphery. A solution to both of these problems, though not one pursued by Stokman and Snijders, is to use some kind of clique or cluster analysis to identify the boundaries of the structural centre if the most central points, for example, constitute a clearly defined and well-bounded 'clique', then it may make sense to regard them as forming the nuclear centre of the graph 7 But not all graphs will have such a hierarchical structure of concentric sets. Where the central points do not cluster together as the nucleus of a
Centrality and centralization 95
centralized graph, the Stokman and Snijders 'centre' will constitute simply a set of locally central, though dispersed, points. In such circumstances, it is not helpful to use the term 'centre'.
It is possible to extend the analysis of centralization a little further by considering the possibility that there might be an 'absolute centre' to a graph. The absolute centre of a graph corresponds closely to the idea of the centre of a circle or a sphere; it is the focal point around which the graph is structured. The structural centre, as a set of points, does not meet this criterion. The absolute centre must be a single point. The centre of a circle, for example, is that unique place which is equidistant from all points on its circumference. By strict analogy, the absolute centre of a graph ought to be equidistant from all points in the graph. This idea is difficult to operationalize for a graph, and a more sensible idea would be to relax the criterion of equidistance and to use, instead, the idea of minimum distance. That is to say, the absolute centre is that point which is 'closest' to all the other points in terms of path distance.
Christofides (1975: Chapter 5) has suggested using the distance matrix to conceptualize and compute the absolute centre of a graph. The beat step in his argument follows a similar strategy to that used by Freeman to measure 'closeness'. Having constructed the distance matrix, which shows the shortest path distances between each pair of points, he defines the eccentricity, or 'separation', of a point as its maximum column (or row) entry in the matrix,' The eccentricity of a point, therefore, is the length of the longest geodesic incident to it. Christofides's first approximation to the idea of absolute centrality is to call the point with the lowest eccentricity the absolute centre. Point B in sociogram (i) of Figure 5.4 has an eccentricity of 1, and all the other points in the graph have eccentricity 2. In this sociogram, then, point B, with the lowest eccentricity, is the absolute centre.9 In other graphs, however, there may be no single point with minimum eccentricity. There may be a number of points with equally low eccentricity, and in these circumstances a second step is needed.
This second step in the identification of the absolute centre involves searching for an imaginay point which has the lowest possible eccentricity for the particular graph. The crucial claim here is that, while the absolute centre of a graph will be found on one of its constituent paths, this place may not Correspond to any actual point in the graph. Any graph will have an absolute centre, but in some graphs this centre will be an imaginary rather than an actual point.
This claim is not so strange as it might at first seem. All the points in sociogram (ii) in Figure 5.4 base eccentricity 2, and so all are
96 Social network analysis
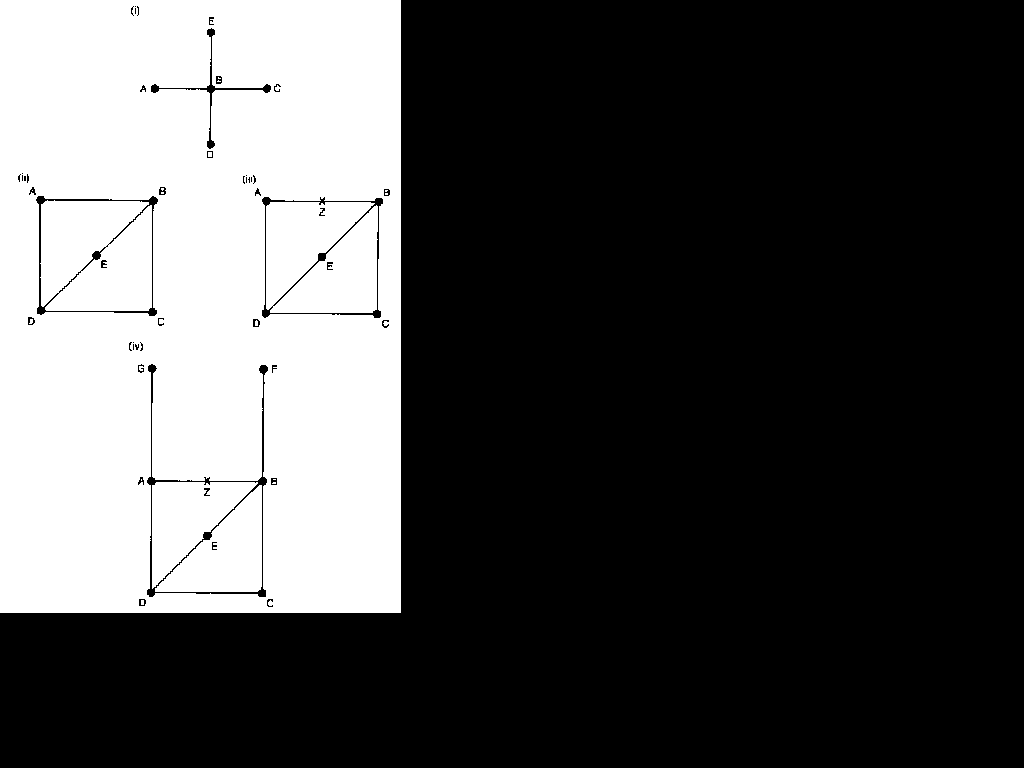
Figure 5.4 The absolute center of a graph
equally 'central'. It is possible, however, to conceive of an imaginary point, Z, which is mid-way between points A and B, as in
Centrality and centralization 97
sociogram (iii), 'Point' Z is distance 0.5 from both A and B, and it is distance 1.5 from points C, D and E. The artificial point Z is more central than any of the actual points, as its eccentricity is 1.5. But it is still not possible to find a single absolute centre for this sociogram. The imaginary point Z could, in fact, have been placed at the midpoint of any of the lines in the sociogram with the same results, and there is no other location for the imaginary point which would not increase its minimum eccentricity. The best that can be said for this graph, therefore, is that there are six possible locations for the absolute centre, none of which corresponds to an actual point. Moving to the second step of searching for an imaginary point as the absolute centre, then, will reduce the number of graphs for which there is no unique absolute centre, but it does not ensure that a single absolute centre can be identified for all graphs. 10
Thus, some graphs will have a unique absolute centre, while others will have a number of absolute centres. Christofides provides an algorithm which would identify, through iteration, whether a graph contains a mid-point or actual point which is its unique absolute centre. " In sociogram (iv) of Figure 5.4, for example, there is a unique absolute centre. Its 'point' Z has an eccentricity of 1.5, compared with eccentricity scores of 2.5 for any other imaginary mid-point, 2 for points A and B, and 3 for points C, D, E, F and G.
A Digression on Absolute Density"
The problem with the existing measures of density, as I showed in the previous chapter, is that they are size-dependent. Density is a measure which is difficult to use in comparisons of graphs of radically different sizes. Density is relative to size. This raises the question of whether it might not be possible to devise a measure of absolute density which would be of more use in comparative studies. I cannot give a comprehensive answer to that question here, but the idea of the absolute centre of a graph does raise the possibility that other concepts required for a measure of absolute density might be formulated along similar lines. A concept of density modelled on that used in physics for the study of solid bodies, for example, would require measures of 'radius', 'diameter' and 'circumference', all of which depend on the idea of the absolute centre.
The radius of a circular or spherical object is the distance from its center to its circumference, on which are found its most distant reachable points. Translating this into graph theoretical terms, the
98 Social network analysis
eccentricity of the absolute centre of a graph can be regarded as the 'radius' of the graph. The 'diameter' of a graph, as will be shown in the following chapter, is defined as the greatest distance between any pair of its points. In sociogram (iv) of Figure 5.4, for example, the radius is 1.5 and the diameter is 3. In this case, then, the diameter is equal to twice the radius, as would be the case in the conventional geometry of a circle or a sphere. This ill not, however, be true for all graphs.
In geometry there is a definite relationship between the area and the volume of a body, these relationships being generalizable to objects located in more than three dimensions. The area of a circle is wr' and the volume of a sphere is 4,r3/3, where w is the ratio of the circumference to the diameter. 'Me general formula for the area of a circle, therefore, is c,21d, and that for the volume of a sphere is 4cr'13d, where c is the circumference, r is the radius and d is the diameter. Applying this to the simple sociogram (iv) of Figure 5.4 would show that it has a volume of 4c(I.5)/9, or 1.5c.'3 But what value is to be given to c in this formula? If the diameter of a graph is taken to be the length of the geodesic between its most distant points (the longest geodesic), the circumference might most naturally be seen as the longest possible path in the graph. In sociogram (iv), this is the path of length 5 which connects point G to point F. Thus, the 'volume' of the example sociogram is 7.5.
Relatively simple geometry has, therefore, enabled us to move a pan of the way towards a measure of the absolute density of a graph in three dimensions. Density in physics is defined as mass divided by volume, and so to complete the calculation a measure of the 'mass' of a graph is required. Mass in physics is simply the amount of matter that a body contains, and the most straightforward graph theoretical concept of mass is simply the number of lines that a graph contains. In sociogram (iv) there are eight lines, and so its absolute density would be 817.5, or 1.06,
Generalizing from this case, it can be suggested that the absolute density of a graph is given by the formula 11(4c,'13d), where I is the number of lines. Unlike the relative density measure discussed in the previous chapter, this formula gives an absolute value which can be compared for any and all graphs, regardless of their size. But one important reservation must be entered: the value of the absolute density measure is dependent on the number of dimensions in which it is measured. The absolute density measure given here has been calculated for graphs in three dimensions. The concept could be generalized to higher dimensions, by using established formulae for 'hyper-volumes', but such an approach would require some agreement about how to determine the dimensionality of a graph. This
Centrality and centralization 99
issue will be approached again in Chapter 8, drawing on the arguments of Freeman (1983).14
Bank Centrality in Corporate Networks
Studies of interlocking directorships among corporate enterprises are far from new, but most of the studies which had been carried out prior to the 1970s had made little use of the formal technique, of social network analysis. Despite some limited use of density measures and cluster analysis, most of these studies twit a strictly quantitative approach, simply counting the numbers of directorships and interlocks among the companies. Levine's influential paper (1972) marked a shift in the direction f this research while, at about the same time, Mokken and his associates in the Netherlands began a pioneering study in the systematic use of graph theory to explore corporate interlocks (Helmets et at., 1975). The major turning point, however, occurred in 1975, when Michael Schwartz and his students presented their major conference paper which applied the concept of centrality to corporate networks (Bearden et a]., 1975). This long paper circulated widely in cyclostyled form and, despite the fact that it remains unpublished, it has been enormously influential. The work of Schwartz's group, and that which it has stimulated, provides a compelling illustration of the conceptual power of the idea of point centrality
Michael Schwartz and Peter Mariolis had begun to build a database of top American companies during the early 1970s, and their efforts provided a pool of data for many subsequent studies (see, for example, Marioiis, 1975; Sonquist and Koenig, 1975). They gradually extended the database to include the top 500 industrial and the top 250 commercial and financial companies operating in the United States in 1962, together with all new entrants to this 'top 750' for each successive year from 1963 to 1973. The final database included the names of all the directors of the 1131 largest American companies in business during the period 1962-73; a total of 13,574 directors. This database is, by any standard, that for a large social network, As such, it lends itself to the selection of substantial sub-sets of data for particular years. One such sub-set is the group of the 797 top enterprises of 1969 which were studied by Mariolis (1975).
The path-bteaking paper of Schwartz and his colleagues (Bearden et at., 1975) drew on the Schwartz Marietta database, and it analysed the data using Granovetter's (1973) conceptual distinction between strong and weak ties. The basis of their argument was that those interlocks which involved the full-time executive officers of
100 Social network analysis
the enterprises could be regarded as the 'strong' ties of the corporate network, while those hich involved only the part-time non-executive directors were its 'weak' ties. The basis of this theoretical claim was that the interlocks which were carried by fulltime executive officers were the most likely board-level links to have a strategic salience for the enterprises concerned. For this reason, they tended to be associated with intercorporate shareholdings and trading relations between the companies." Interlocks created by non-executive directors, on the other hand, involved less of a time commitment and so had less strategic significance for the enterprises concerned,
The top enterprises were examined for their centrality, using Bonacich's (1972) measure. This, it will be recalled, is a measure in which the centrality of a particular point could be measured by a combination of its degree, the value of each line incident to it, and the centrality of the other points to which it is connected. This is a ,recursive', circular measure which, therefore, requires a considerable amount of computation. A network containing 750 enterprises, for example, will require the solution of 750 simultaneous equations. The first step in Bearden et al.'s analysis was to decide on an appropriate measure for the value of the lines which connected the enterprises. For the weak, undirected lines, Bearden et al. held that the value of each should be simply the number of separate interlocks, weighted by the sizes of the two boards. This weighting rested on the supposition that having a large number of interlocks was less significant for those enterprises with large boards than it was for those with small boards. The formula used in the calculation was bij/SQRT(didj), where bij is the number of interlocks between the two companies i and j, and di and dj are the sizes of their respective boards. This formula allows Bonacich's centrality measure to be calculated on the basis of all the 'weak ties' in the graph.
A more complex formula was required to measure centrality in terms of the strong ties. In this case, the measure of the value of each line needed to take some account of the direction which was attached to the lines in the graph. For those companies which were the 'senders' of lines (the 'tails', in the terminology of the GraDAP program) the value of the lines was calculated by the number of directors 'sent', weighted by the board size of the 'receiving' company. The attempt in this procedure was to weight the line by the salience of the interlock for the receiving board. Conversely, for those companies which were the 'receivers' of interlocks (the 'heads'), the number of directors received was weighted by the sender's board size, 16 For the final calculation of centrality scores,
Centrality and centralizationi 101
Bearden el al. introduced a further weighting. Instead of taking simply the raw weighted scores for the tails and the heads, they took 90 per cent of the score for the senders and 10 per cent of the score for the recipients. The reasoning behind this weighting of the scores was the theoretical judgement that, in the world of corporate interlocking, it is 'more important to give than to receive': the sending of a director was more likely to be a sign of corporate power than was the receiving of a directorship. Thus, the arbitrary adjustment to the centrality scores was introduced as a way of embodying this judgement in the final results.
The Bonacich measure of centrality which was calculated for the companies in the study correlated very highly, at 0.91, with the degrees of the companies. Bearden et al. held, however, that the more complex Bonacich measure was preferable because it had the potential to highlight those enterprises which had a low degree but which were, nevertheless, connected to highly central companies. Such a position, they argued, may be of great importance in determining the structural significance of the companies in the economy.
Schwartz and his colleagues also used a further approach to centrality, which they termed 'peak analysis'. This was later elaborated by Mizruchi (1982) as the basis for an interpretation of the development of the American corporate network during the twentieth century. A point is a peak, it was argued, if it is more central than any other point to which it is connected. Mintz and Schwartz (1985) extend this idea by defining a bridge as a central point which connects two or more peaks (see Figure 5.5). They further see a 'cluster' as comprising all the direct contacts of a peak, except for those which have a similar distance I connection to another peak. Thus, peaks lie at the hearts of (heir clusters.,,
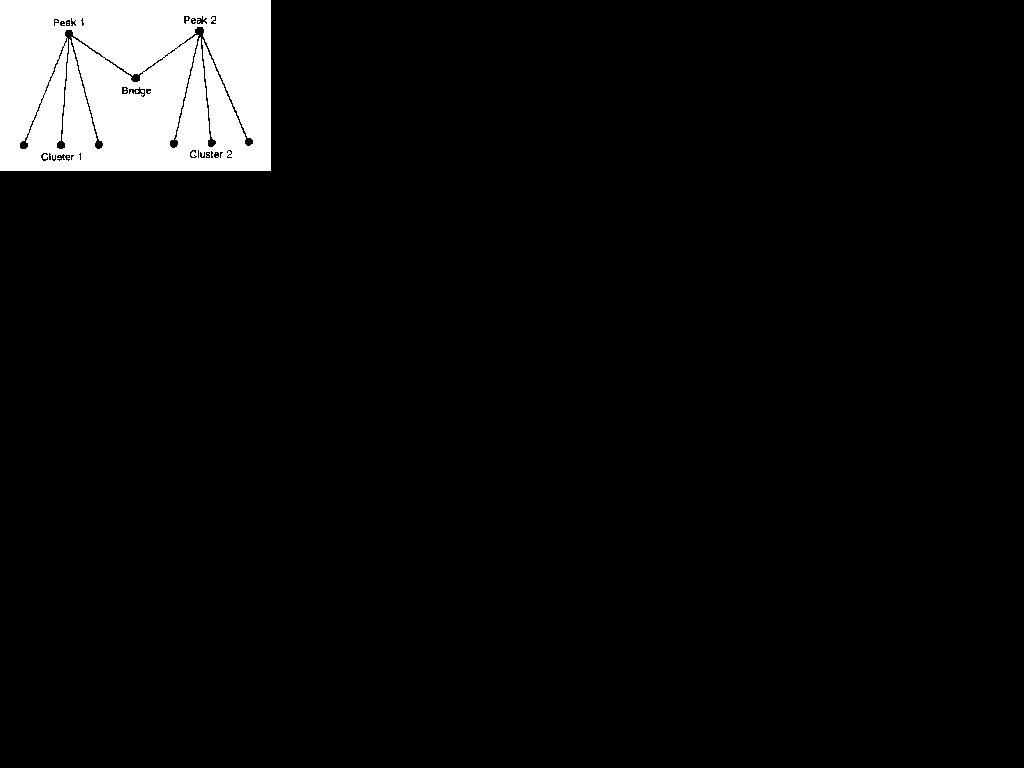
Figure 5.5 Peaks and Bridges
102 Social network analysis
The results which were arrived at through the use of these techniques for the measurement of point centrality have become widely accepted as indicating some of the most fundamental features of intercorporate networks. In summary, Bearden et al. argued that the American intercorporate network showed an overall pattern of 'bank centrality': banks were the most central enterprises in the network, whether measured by the strong or the weak ties. Bank centrality was manifest in the co-existence of an extensive national interlock network (structured predominantly by weak ties) and intensive regional groupings (structured by the strong ties). Strong ties had a definite regional base to them. The intensive regional clusters were created by the strong ties of both the financial and the non-financial enterprises, but the strong ties of the banks were the focal centres of the network of strong ties. The intercorporate network of 1962, for example, consisted of one very large connected components two small groupings each of four or five enterprises, and a large number of pairs and isolated enterprises. Within the large connected component, there were five peaks and their associated clusters, The dominant element in the network of strong ties was a regional cluster around the Continental Illinois peak, which, with two other Chicago banks, was connected with a group of II mid-Western enterprises with extensive connections to a larger grouping of 132 enterprises. The remaining four peaks in the network of strong ties were Mellon National Bank, J.P. Morgan, Bankers Trust and United California Bank, their clusters varying in size from four to ten enterprises.
Overlying this highly clustered network of strong, regional ties was an extensive national network created by the weak ties which linked the separate clusters together. This national network, Bearden et al. argued, reflected the common orientation to business art airs and a similarity of interests which all large companies shared. Interlocks among the non-executive directors expressed this commonality and produced integration, unity and interdependence at the national level (see also Useem, 1984). The great majority of the enterprises were tied into a single large component in this network, most of the remainder being isolates. Banks were, once more, the most central enterprises, especially those New York banks which played a 'national' rather than a 'regional' role. It was the nonexecutive directors of the banks who cemented together the overall national network.