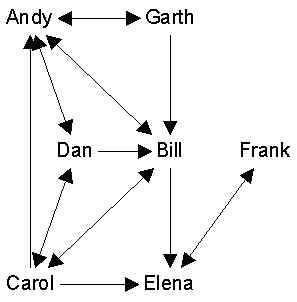
Networks can be represented as graphs or matrices. For example, here is a graph:

We can also record who is connected to whom on a given social relation via what is called an adjacency matrix. The adjacency matrix is a square actor-by-actor matrix like this:
| And | Bil | Car | Dan | Ele | Fra | Gar | |
| Andy | 1 | 0 | 1 | 0 | 0 | 1 | |
| Bill | 1 | 1 | 0 | 1 | 0 | 0 | |
| Carol | 1 | 1 | 1 | 1 | 0 | 0 | |
| Dan | 1 | 1 | 1 | 0 | 0 | 0 | |
| Elena | 0 | 0 | 0 | 0 | 1 | 0 | |
| Frank | 0 | 0 | 0 | 0 | 1 | 0 | |
| Garth | 1 | 1 | 0 | 0 | 0 | 0 |
If the matrix as a whole is called X, then the contents of any given cell are denoted xij. For example, in the matrix above, xij = 1, because Andy likes Bill. Note that this matrix is not quite symmetric (xij not always equal to xji).
Anything we can represent as a graph, we can also represent as a matrix. For example, if it is a valued graph, then the matrix contains the values instead of 0s and 1s.
By convention, we normally record the data so that the row person "does it to" the column person. For example, if the relation is "gives advice to", then xij = 1 means that person i gives advice to person j, rather than the other way around. However, if the data not entered that way and we wish it to be so, we can simply transpose the matrix. The transpose of a matrix X is denoted X'. The transpose simply interchanges the rows with the columns.
Matrix Algebra
Matrices are basically tables. They are ways of storing numbers and other things. Typical matrix has rows and columns. Actually called a 2-way matrix because it has two dimensions. For example, you might have respondents-by-attitudes. Of course, you might collect the same data on the same people at 5 points in time. In that case, you either have 5 different 2-way matrices, or you could think of it as a 3-way matrix, that is respondent-by-attitude-by-time.
Notice that the rows and columns point to different class of entities. Rows are people, and columns are properties. Each different class of entities in a matrix is known as a mode. So this matrix is 2-way and 2-mode. Suppose we had a different matrix. Say we recorded the number of times that each of you spoke to each other of you. This would be a person-by-person matrix, which is 2-way 1-mode. If we tallied this up each month, we would have a person-by-person-by-month matrix, which would be 3-way, 2-mode.
A 1-way matrix is also called a vector. If it has rows but just one column, its a column vector. If it has columns but just one row its a row vector.
Typically, we refer to matrices using capital letters, like X. The number in a particular cell is identified via small letters and subscripts. Like x2,3. A generic cell in some row or some column is xij.
Although matrices are collections of numbers, they are also things in themselves. There are mathematical operations that you can define on them. For example, there is the transpose A’ where the rows become columns and vice versa.
For example, you can add them:
C = A+B
You can only perform these operations on matrices that are conformable. This means that they are of compatible sizes. Usually, that means they are the exact same size. For example, to add or subtract matrices, they must be the same size.
Multiplying matrices is a whole different thing. You write it this way: C=AB. First of all, you should know that matrix multiplication is not commutative. That is, it is not always true that AB=BA
Second, conformable in matrix multiplication means that the number of columns in the first matrix must equal the number of rows in the second.
Third, the product that results from a matrix multiplication has as many rows as the first matrix and as many columns as the second. so
A * B = C
3x2 * 2x4 = 3x4
Let A be
| 1 | 2 |
| 3 | 4 |
| 1 | 0 |
and B be
| 1 | 1 | 2 | 2 |
| 2 | 2 | 4 | 4 |
then C = AB is:
| 1*1+2*2 | 1*1+2*2 | 1*2+2*4 | 1*2+2*4 |
| 3*1+4*2 | 3*1+4*2 | 3*2+4*4 | 3*2+4*4 |
| 1*1+0*2 | 1*1+0*2 | 1*2+0*4 | 1*2+0*4 |
or
| 5 | 5 | 10 | 10 |
| 11 | 11 | 22 | 22 |
| 1 | 1 | 2 | 2 |
Note that we could not even try to multiply B*A, because they are not conformable.
What happens if we multiply A by matrix I which looks like this:
| 1 | 0 |
| 0 | 1 |
You get A back again! I is known as the identity matrix. It has 1s down the diagonal, and zeros elsewhere. Its almost always called I. When you multiply it by any matrix, you always get that matrix back again.
Now suppose you have an equation like
C = AB
and you have measured the values for C and for B, and would like to solve for the values of A. Can you do it?
Yes, but you can’t divide both sides by B. You can’t divide matrices at all. Just can’t do it. But you can multiply by the multiplicative inverse.
An inverse of an ordinary number is that thing you have to multiply the number by to get 1. The inverse of 2 is 0.5, because if you multiple 2*.5 you get 1.
In matrices, the inverse of B of is a matrix B-1 which when multiplied by B gets the identity matrix I, which is the matrix with all ones down the diagonal and zeros elsewhere.
If AB=BA=I, then A = B-1
So to find A in the equation C=AB, you postmultiply both sides by the inverse of B and get CB-1 = A.
This only works if B is square: same number of rows and columns.
Also, B must be non-singular. This means that none of the columns can be computed as a linear combination of any of the other columns. Same with the rows.
Postmultiplying matrix by a vector (Xb) is like computing weighted sum of rows. averaging across columns. if b is 1, then is just row sums. To get column sums, do btX or (Xtb)t
Eigenvectors and eigenvalues. The defining equation is Xv = kv, or kv = Xv, or v = k-1Xv or vi = k-1 xijvj