Homework Assignment
Network Puzzle

In the Bavelas-Leavitt experiments, the circle configuration (see figure below) did not perform very well. This is surprising because theoretically it can transmit information to all parties much faster than all the other configurations. In fact, it can solve the puzzle in 3 units of time, whereas the star (aka wheel) requires a minimum of 5 units of time.

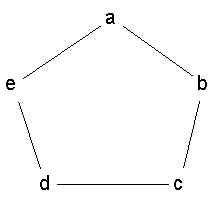
Your task is to show how the circle can solve the puzzle in 3 units of time. Recall the rules:

• First, each person at the start of the round is given a unique piece of information.
• Second, at any given moment in time, each node can transmit information to only one other person, but they can receive messages from several people at the same time. For example, at Time 1, b can send a message to a, but that precludes sending a message to c at that time. However, also at Time 1, a and c can both choose to send a message to b, so that at the end of Time 1, b has information from both a and c (and herself), and she has given information to a.
• Third, at any given moment, you can transmit as much information as you already have (i.e., had acquired at the end of the previous round).

Your job is to figure out what is the minimum number of units of time required so that every person has everyone else's unique information.