The Standard Deviation

When you measure any interval or ratio-level variable, you usually get variation (if every person had  the same value on some variable, it would not be a very useful variable to measure). There is always a mean value, but there is also always "spread" around that mean: some values are bigger than the mean, others are smaller. The standard deviation (SD) says how far away numbers in a list typically are from their average.

The standard deviation is an estimate of the magnitude of deviations from the mean. Consider a list of numbers with a certain mean. Each number in the list deviates from the average by some amount, including 0. For each number we can compute the amount of deviation from the average by subtracting the average from each number. This creates a new list of numbers (a new variable). The SD of the original list, is just the RMS of the deviations variable. In other words, we defined SD as:

SD = SQRT(average of (deviations from average)²)

Example. Find the SD of the list 20, 10, 15, 15.

Solution. The first step is to find the average:

average = (20 + 10 + 15 + 15)/4 = 15.

The second step is to find the deviations from the average: just subtract the average from each entry. The deviations are

5, -5, 0, 0

The last step is to find the RMS of the deviations:

SD = SQRT[ (5²+ (-5)² + 0² + 0²)/4 ]

= SQRT[ (5+25+0+0)/4 ]

= SQRT[12.5] = 3.5

The SD comes out in the same units as the data. For example, if heights are measured in inches then the SD comes out in inches too. The intermediate squaring step in the procedure changes the units to inches squared, but the final step of taking the square root returns the answer to the original units.

Important: Don't confuse the SD of a list with the RMS of the list. The SD is the RMS, not of the original numbers on the list, but of their deviations from average.

Example

There was a study called the HANES study which looked at physical characteristics of Americans. In the sample, there were 6,588 women age 18-74. Their average height was 63.5 inches, and the SD of height was 2.5 inches. The average tells us that most of the women were somewhere around 63.5 inches tall. But there were deviations from the average. Some of the women were taller than average, some shorter. The SD tells how big these deviations were. The SD says how far away numbers in a list typically are from their average. Most values in the list will be within one SD (2.5 inches) of the average. Very few values will be more than two or three SDs away from the average.

When a variable is normally distributed (so that the frequency distribution is bell-shaped, as in the figure below), roughly 68% of the entries on a list (around two thirds) are within one SD of the average (including both directions), the other 32% are further away. Roughly 95% (19 in 20) are within two SDs of the average, the other 5% are further away. Many variables are more or less normally distributed, so this rule of thumb works for most lists of numbers, though not all.

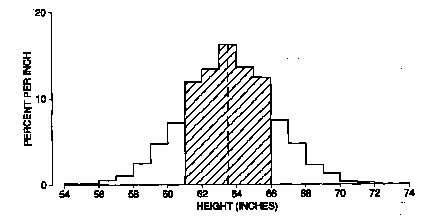
Figure 1. The SD and the histogram for the heights of the 6,588 women age 18-74 in the HANES sample. The average of 63.5 inches is marked by a dashed vertical line. The region within one SD of the average is shaded: 67% of the women differed from average by one SD (2.5 inches) or less. (From Statistics, by Freedman, Pisani, Purves, Adhikari)

With the HANES data, 67% of the women differed from the average height by one SD or less, and 94% differed from average by two SDs or less. There was only one woman in the sample who was more than four SDs away from the average. For this data set, the rule of thumb works quite well. The histogram is shown in the figure above. The average is marked by a vertical line, and the region within one SD of the average is shaded.

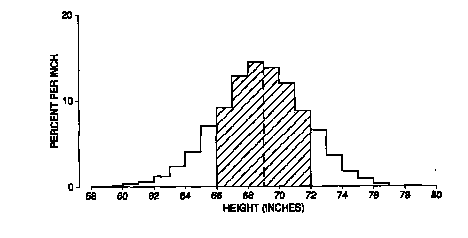
Figure 2. The SD and the histogram for the heights of the 5,916 men age 18-74 in the HANES sample. The average of 69 inches is marked by a dashed vertical line. The region within one SD of the average is shaded; 71% of the men differed from average by one SD (3 inches) or less. (From Statistics, by Freedman, Pisani, Purves, Adhikari)

The next example is the heights of the sample men. The average height was 69 inches; the SD was 3 inches. Figure 2 shows the histogram. With respect to height, 71 % of the men differed from the average by less than one SD, and 96% differed from the average by less than two SDs. No man differed from the average by more than four SDs. Again, the 68%-95% rule works quite well.

Where do the figures of 68% and 95% come from? Stay tuned...

(Based on Statistics, by Freedman, Pisani, Purves, Adhikari).