Algebraic Analysis of Coded Data
Drawn from Charles C. Ragin, 1987. The Comparative Method. University of California Press.
Ragin and Strauss/Glaser come out of the same methodological milieu. Both are steeped in a case-oriented tradition (rather than variable-oriented), they feel that comparison is the fundamental analytic act, they work with large amounts of (coded) text, they seek to induce theory from data rather than deduce facts from theory, they are not enamored by statistical approaches, and want to develop a rigorous, formal method of deriving theory.
Ragin opens his book with this quote from Swanson "Thinking without comparison is unthinkable. And in the absence of comparison, so is all scientific thought and scientific research." Part and parcel of the comparative approach is the notion of categories and instances, just as in grounded theory. Ragin says: "consider an investigation which concludes that a strong relationship between social class and party preference exists in Great Britain because 'Great Britain is an industrial society'. This conclusion concretizes the term society by providing an example (Great Britain) and by implying that there are other societies, some of which are industrial and some of which are not." This is just like grounded theory.
Also like grounded theory, Ragin recommends what Glaser and Strauss call theoretical sampling, saying the following:
This means that the comparative method does not work with samples or populations but with all relevant instances of the phenomenon of interest and, further, that the explanations which result from applications of the comparative method are not conceived in probabilistic terms because every instance of a phenomenon is examined and accounted for if possible. Consequently, the comparative method is relatively insensitive to the relative frequency of different types of cases. For example, if there are many instances of a certain phenomenon and two combinations of conditions that produce it, both combinations are considered equally valid accounts of the phenomenon regardless of their relative frequency. If one is relatively infrequent, an application of the statistical method to this same set of data might obscure its existence. The comparative method would consider both configurations of conditions relevant since both result in the phenomenon of interest.
In other words, in collecting data it is theoretically important to obtain as much diversity of cases as possible, rather than achieving representativeness.
The comparative method is based on John Stuart Mill's (1943) three methods of inductive inquiry: the method of agreement, the method of difference, and the indirect method of difference. The method of agreement says that if several instances of a phenomenon under investigation have certain conditions or potential causes in common, then those conditions that in common are the ones that are the real causes. So to find out what causes something, you collect many instances of it, and find the condition(s) that always precede the appearance of the phenomenon of interest. Mill cautioned against liberal use of this method, saying that experimental designs (which he called the method of difference) were preferable when feasible.
The method of difference, as applied to natural settings rather than the laboratory, involves collecting a number of cases which are identical except for one causal condition (the treatment variable) and the outcome variable. For example, Russia in 1905 resembled Russia in 1917 in most respects. What key differences account for the greater success of the 1917 revolt?
The indirect method of difference consists of a double application of the method of agreement, once on the positive cases, and once on the negative. For example, to investigate whether rapid commercialization causes peasant revolts, the researcher first identifies instances of peasant revolt to see if they all have rapid commercialization. If they do, then instances of the absence of peasant revolts (among peasant societies) are examined to see if they agree in displaying an absence of rapid commercialization. The key is that both negative and positive cases are considered.
This last approach sounds statistical: it corresponds to examining association in a 2-by-2 table. However, Ragin is not a fan of statistical approaches, on technical grounds alone:
Smelser's argument implies that the comparative method is inferior to the statistical method. Is it? The comparative method is superior to the statistical method in several important respects. First, the statistical method is not combinatorial; each relevant condition typically is examined in a piecemeal manner. Thus, for example, the statistical method can answer the question: what is the effect of having a history of class struggle net of the effect of industrialization? But it is difficult to use this method to address questions concerning the consequences of different combinations of conditions (that is, to investigate situations as wholes). To investigate combinations of conditions, the user of the statistical method must examine statistical interactions. The examination of a large number of statistical interactions in variable- oriented studies is complicated by collinearity and by problems with scarce degrees of freedom, especially in comparative research where the number of relevant cases is often small. An exhaustive examination of different combinations of seven preconditions, for example, would require a statistical analysis of the effects of more than one hundred different interaction terms.
Ragin wants to create a method has the strengths of both case-orientation and variable-orientation. It should handle many cases, to avoid the charge of particularism. It should embody the logic of experimental design as much as possible. It must recognize that some causes affect other causes, and so must deal with combinations of conditions. It should provide a means of simplification and data reduction that, unlike statistical methods, does not simply throw out rare cases. It should allow for alternative explanations. A weakness of case-oriented studies is that:
A case-oriented investigator labors in isolation to produce a study which, in the end, bears his or her mark. Typically, a case-oriented study elaborates the ideas and theories of the investigator with data that are not generally known or accessible to other investigators, and often only perfunctory consideration of alternative explanations and arguments is offered. In essence, case-oriented analyses usually stack the deck in favor of the preferred theory.
In contrast, variable-oriented studies are more consonant with scientific method, but tend to throw away ideas as theories are discarded that don't fit the data.
How can we trust the results of boolean algebra? Does solving a boolean algebra equation actually have theoretical meaning? Yes. The algebra is just a shortcut. Nothing is done that wouldn't be done by the human mind. It is similar to the issue of trusting division.
Suppose you have 55 candies to be divided equally among 5 people. How many candies should each person get? One way to solve this would be to think it through "logically", rather than arithmetically. If there were 5 candies, then each person should get one. If there were 10 candies, then that's just the same problem twice, so each person gets 2 candies in total. If there were 20 candies, that's the previous operation twice, so that's a total of 4 candies per person. If there were 40 candies, that's 8 candies per person. But there are 55 candies, so that's another three rounds of the initial game with 5 candies, so that would be a total of 8 + 3 = 11 candies per person.
An alternative approach would be use long division: 5 goes into the first 5 once, with 0 left over. Now we divide the other 5 by 5 and get 1 again, so that's 11.
The same is true of multiplication. You can deal with it mechanically, as we usually do, or we can think in terms of multiple sets of a objects. For example, to multiply 12 by 6, we can mechanically do this:
| 1 | |
| 1 | 2 |
| 6 | |
| -- | -- |
| 7 | 2 |
The process of multiplying the 2 by the 6 and then carrying the one is mysterious. But it does work. We could instead think about having 6 sets of 12 items. So we could compute the 72 by counting: here's 12, here's 24, here's 36 all the way to 72. The important thing is that we don't have to think of it this way: the mechanical way allows us to deal with very large quantities quite effortlessly.
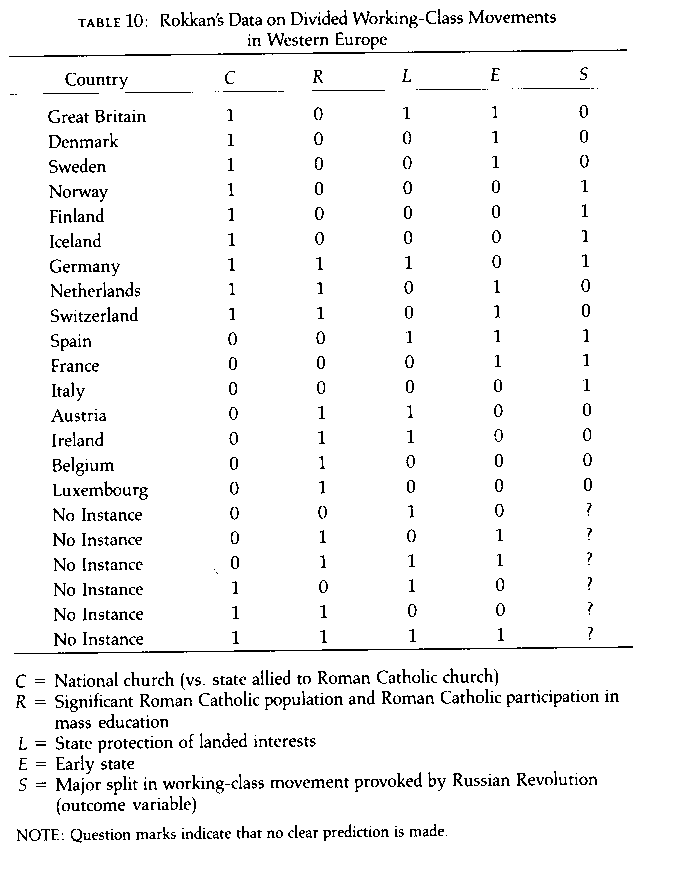
First step is to code text or behavior into presence/absence variables. The raw data is a case-by-code matrix (see table 10).

The next step is to group these cases by pattern, so that all the cases with exactly the same conditions and outcomes are grouped together, and counted, as in Table 5. Note that in the table, the rows are no longer cases -- they are distinct combinations of codes, and all possible combinations are listed.
Table 5: Hypothetical Truth Table showing 3 causes of successful strikes
| Causes | Outcome | Freq. | ||
| A | B | C | S | F |
| 1 | 0 | 1 | 1 | 6 |
| 0 | 1 | 0 | 1 | 5 |
| 1 | 1 | 0 | 1 | 2 |
| 1 | 1 | 1 | 1 | 3 |
| 1 | 0 | 0 | 0 | 9 |
| 0 | 0 | 1 | 0 | 6 |
| 0 | 1 | 1 | 0 | 3 |
| 0 | 0 | 0 | 0 | 4 |
Now we need to review some basic boolean algebra.
OR and AND in Boolean Algebra:
We can describe all the cases in Table 5, using boolean AND and OR operators. The AND is written like multiplication: letters are next to each other if they have an AND relation. The OR is written like addition: a plus sign between them.
So we can describe the first category of cases in the strike data (6 of them) as having this pattern of conditions:
AbC
That means: A is present AND B is absent AND C is present. The second set of cases is written:
aBc
To refer to both sets of cases together, we can write:
AbC + aBc
That means: 'we are considering all those cases in which there is a booming product market and no threat of sympathy strikes and there is a large strike fund, OR there is no booming product market, there is a threat of sympathy strikes, and there is no large strike fund.
We can summarize all the cases in which there are successful strikes as:
S = AbC + aBc + ABc + ABC
Note that the use of algebraic notation is a convenience (which will lead to additional conveniences) but is just notation: the equation says nothing more than what one could say in words: of the all the known cases of successful strikes, there are four categories: the first category consists of strikes in which there was a booming product market, no significant threat of sympathy strikes, and a large strike fund, the second category ... etc.
Some Special Cases
If you multiply b times B, you get nothing -- the result just disappears. This is because there can be no cases in which you have B and b at the same time -- existence and non-existence simultaneously.
Also, if you multiple B times B, you just get B -- that is all cases that are both B and B. So B=BB.
Presence and absence of conditions are equally important. Both can viewed as causes. For example, in row 2, B seems to cause S. Or is that the absence of A and C causes S? Presence and absence should be viewed as conditions that lead to the outcome. Depending on the data in the other rows, it may be that it is the combination of B being present and A and C being absent that causes S..
Principle of Minimization
If two expressions differ by one condition but produce the same outcome, that condition that distinguishes them can be considered irrelevant, and removed. This is analogous to controlling for other variables in experimental design.
Note that nothing has been lost here: eliminating redundancy does not change anything, it just makes things easier to grasp. Suppose I said 'To get to BC from Natick on Tuesdays it is best to take Route 9', and you asked what about Wednesday's? And I said 'route 9' and you asked about every other day, and the answer is always route 9. Rather than represent that by writing seven nearly identical sentences, one for every day, it is simpler to say "To get to BC from Natick it is best to take Route 9'. In this context, the sentence implies that no matter what day it is, route 9 is always the best.
For the data in our running example, this process of elimination results in the following simplified equation:
S = AC + AB + Bc
How do you get there? One approach is to compare each 3-character term in the full equation and look for pairs that differ by just one character. For example, AbC and ABC share AC, so evidently, it doesn't matter what state the B/b variable is in. Here's a way to record the simplications (let's call this the "implication table"):
| contains: | AbC | aBc | ABc | ABC |
| AC | 1 | 0 | 0 | 1 |
Similarly ABc and ABC share AB, so we record that in the matrix:
| contains: | AbC | aBc | ABc | ABC |
| AC | 1 | 0 | 0 | 1 |
| AB | 0 | 0 | 1 | 1 |
Finally, aBc and ABc share Bc:
| contains: | AbC | aBc | ABc | ABC |
| AC | 1 | 0 | 0 | 1 |
| AB | 0 | 0 | 1 | 1 |
| Bc | 0 | 1 | 1 | 0 |
So the equation S = AC + AB + Bc "covers" the original equation, saying exactly the same thing but with fewer and simpler terms. Make no mistake that it is the same. For example, having AC in the equation implies that both AbC and ABC both lead to success, which is true. Similarly, since AB is there, ABc and ABC both lead to success, and finally, Bc implies that ABc and aBc lead to success. So from S = AC + AB + Bc, we can get
S = AbC + ABC + ABc + aBc
which is exactly what we started with.
Sometimes this process results in redundant prime implicants. We can invoke principle of parsimony to delete unnecessary elements.
S = AC + Bc
How do we get there? Just look at the last "implication" table above. Notice that if we delete the AB row, we are still left with a table in which every column is "covered" -- i.e., has a 1 in it somewhere:
| contains: | AbC | aBc | ABc | ABC |
| AC | 1 | 0 | 0 | 1 |
| Bc | 0 | 1 | 1 | 0 |
This means that AC and Bc are sufficient to generate all of the more complicated terms in the columns. So we didn't need the AB row -- it was superfluous.
Note again that this simplified phrase implies the more complicated one: nothing has been lost. AC implies AbC and ABC. Bc implies ABc and aBc. Together that gives:
S = AbC + ABC + ABc + aBc
which is again what we started with.
It is always possible that in doing the algebraic manipulation, you made a mistake: perhaps a typo. So perhaps we should check our final sentence (S = AC + Bc). If it's right, then every case of successful strikes in the data should have either AC (booming market and large strike fund) or Bc (threat of sympathy strikes and small strike fund). Here are the data again:
| Combo | A | B | C | _ | S |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 1 | |
| 2 | 0 | 1 | 0 | 1 | |
| 3 | 1 | 1 | 0 | 1 | |
| 4 | 1 | 1 | 1 | 1 | |
| 5 | 1 | 0 | 0 | 0 | |
| 6 | 0 | 0 | 1 | 0 | |
| 7 | 0 | 1 | 1 | 0 | |
| 8 | 0 | 0 | 0 | 0 |
The first four combinations correspond to successful strikes. Combination 1 is an example of AC, so it fits. Combination 2 is a Bc. Combo 3 is another Bc, and Combo 4 is an AC. So all four combinations that lead to successful strikes are correctly described as being either AC or Bc.
What about the unsuccessful strikes? Is our simplified description subject to Type II error, so that it also includes cases that were unsuccessful? Well, Combo 5 is neither AC nor Bc. Combo 6 is neither. Combo 7 is neither. And Combo 8 is also neither AC nor Bc. So the formula S = AC + Bc is perfect: it describes all the successful, and excludes all the unsuccessful strikes.
de Morgan’s Law of Negation
de Morgan's law tells you how to negate a boolean expression -- how to get the complement of cases. So if S = AC + Bc, de Morgan's law can tell you what little "s" equals, i.e., give you a description of the unsuccessful strikes. To apply de Morgan's law, you just make call capitals into lowercase (and vice-versa) and all multiplications into additions (and vice-versa). So AB becomes a+b and CA+CB becomes (c+a)(c+b). So ...
s = (a+c)(b+C) = ab + aC + bc
So unsuccessful strikes come in three types.
As an aside, negation might help to understand what happens when you multiply b times B. The result is bB. If we negate that, we get B+b. So what is B+b? that is any case in which B is either present or absent, which would be all cases, regardless of any other variables. So negating that in turn (which gets bB) must be the opposite, which is no cases.
Necessity and Sufficiency
In F = AC + BC = C(A+B), C is necessary but not sufficient (either A or B must also be present).
In S = AC + Bc, nothing is either necessary or sufficient. In F = A + Bc, A is sufficient but not necessary.
In F = B, B is both necessary and sufficient.
Factoring for Interpretation
Suppose we have this:
S = abc + AbC + abd + E
Now, if we like, we can replace E with aE and AE:
S = abc + AbC + abd + aE + AE
(Note that E implies aE and AE, so writing aE+AE is the same thing as writing just E)
S = a(bc+bd+E) + A(bC+E)
This highlights what is needed when A is present and what is needed when A is absent.
The Problem of Limited Diversity
In table 7, there are two rows that are missing, in the sense that no cases were observed with certain combinations of conditions.

Using just the rows we have cases for, F = abC + aBC + AbC. Factoring,
| abC | aBC | AbC | |
| aC | 1 | 1 | 0 |
| bC | 1 | 0 | 1 |
So,
F = aC + bC = C(a+b).
This says that Erosion of ethnic institutions is a necessary (but not sufficient) cause of party formation
But implicitly, this assumes that in the missing cases, there are not parties formed -- i.e., these are the only ways to achieve F. And since the missing cases are the ones in which both A and B are present, we really donít know what happens when A and B are both present. If the last case is a 1, then we have
F = abC + aBC + AbC + ABC
Factoring,
| abC | aBC | AbC | ABC | |
| aC | 1 | 1 | 0 | 0 |
| bC | 1 | 0 | 1 | 0 |
| AC | 0 | 0 | 1 | 1 |
(dropping bC for parsimony), we have
F = aC + AC
F = C
Before, we knew C was important, but had to assume that C needed to work in concert with the the absence or A or the absence of B. Now, however, we know that a more general model (which includes our first model as a special case) explains all the cases.
Now, if it was the other missing case that was a 1 instead, then we have
F = aC + bC + ABc
If both the last cases are 1, then we have
F = abC + aBC + AbC + ABc + ABC
Factoring,
| abC | aBC | AbC | ABc | ABC | |
|---|---|---|---|---|---|
| aC | 1 | 1 | 0 | 0 | 0 |
| bC | 1 | 0 | 1 | 0 | 0 |
| AC | 0 | 0 | 1 | 0 | 1 |
| AB | 0 | 0 | 0 | 1 | 1 |
We then have
F = aC + bC + AC + AB
and factoring again,
| aC | bC | AC | AB | |
| C | 1 | 1 | 1 | 0 |
which leaves
F = C + AB
Comparing this with our original (F = aC + bC ), we see again that this includes our original model as a special case.
We can use the methodology to analyze the difference between the present and absent cases, by creating new outcome variable: present vs absent. So we create a new dependent variable which is "1" for all combinations of independent variables that we have cases for, and is "0" for all combinations that are missing. The data for Table 7 are given again below. A new column has been added called "E" to indicate cases in existence
Table 7
| Combo | A | B | C | _ | F | E |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 1 | |
| 2 | 0 | 0 | 1 | 1 | 1 | |
| 3 | 0 | 1 | 0 | 0 | 1 | |
| 4 | 0 | 1 | 1 | 1 | 1 | |
| 5 | 1 | 0 | 0 | 0 | 1 | |
| 6 | 1 | 0 | 1 | 1 | 1 | |
| 7 | 1 | 1 | 0 | ? | 0 | |
| 8 | 1 | 1 | 1 | ? | 0 |
A = Ethnic inequality
B = Centralized government
C = Erosion of ethnic institutions
F = Formation of ethnic parties
E = Cases exist for this combo
So,
E = abc + abC + aBc + aBC + Abc + AbC
Factoring,
| abc | abC | aBc | aBC | Abc | AbC | |
|---|---|---|---|---|---|---|
| ab | 1 | 1 | 0 | 0 | 0 | 0 |
| ac | 1 | 0 | 1 | 0 | 0 | 0 |
| bc | 1 | 0 | 0 | 0 | 1 | 0 |
| aC | 0 | 1 | 0 | 1 | 0 | 0 |
| bC | 0 | 1 | 0 | 0 | 0 | 1 |
| aB | 0 | 0 | 1 | 1 | 0 | 0 |
| Ab | 0 | 0 | 0 | 0 | 1 | 1 |
We then have
E = ab + ac + bc + aC + bC + aB + Ab
and factoring again,
| ab | ac | bc | aC | bC | aB | Ab | |
|---|---|---|---|---|---|---|---|
| a | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| b | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
We get E = a + b. And by de Morgan's law, the nonexistents are e = AB, confirming what, in this case, we could see directly.
In table 8, analyzing presence of cases gives P = ac + aD + BD + Abd, which says there are 4 basic types of peasant societies. That is interesting in itself. Only 4 kinds of peasant societies. Why is that?
Now let's look at the which societies have peasant revolts. After doing the algebra, it turns out that R = ABD + aCD. This is a subset of the equation for societies that exist. (That's comforting: revolts only occur in societies that actually exist.) To see why the second equation is a subset of the first, note that BD includes (i.e., implies) ABD, and that aD includes aCD. So revolts are found in only two of the four basic kinds of peasant societies.

Resolving Contradictory Data
Example is 4th row of the data (table 9). There are 10 cases with this combination of conditions, of which 3 have revolts and 7 do not. So how do we code this? Until now, we have assumed that all the cases corresponding to a given combination of conditions had the same value on the dependent variable. But sometimes, this is not the case. Why not? could be measurement error. Or, more likely, you do not have all the important independent variables. You are missing a 5th variable that is distinguishing between the cases that are the same on the other 4 variables.

How to proceed? The first thing to do is to analyze the combinations with inconsistent outcomes. What characterizes those cases? Similarly, what characterizes the cases with perfectly consistent outcomes? In the case of Table 9, consider the combinations (marked with "?") in which the outcome is very unclear (near equal split of revolt and no revolt). Let us model just those 4 combinations:
? = Abcd + AbCd + ABcD + ABCD
Factoring,
| Abcd | AbCd | ABcD | ABCD | |
|---|---|---|---|---|
| Abd | 1 | 1 | 0 | 0 |
| ABD | 0 | 0 | 1 | 1 |
So, ? = Abd + ABD = A(bd + BD). Since A = peasant traditionalism, this suggests examining (a) what exactly is meant by this code (maybe it's two codes in one), and (b) looking for variables that combine with peasant traditionalism to create revolution.
(many other possibilities follow)
Evaluating Theoretical Arguments
Any theory can be expressed as boolean equation. For example, Allport's theory of prejudice says that ICD+PCD=J, where the letters stand for the following variables: Inequality, Contact, iDentifiability, comPetition, preJudice. We can compare the equation with the one determined by data. By multiplying the two (theory and observed equations) together, we can see what they have in common, and therefore which parts of the theory were borne out).
A more interesting approach is to examine observed cases that were not predicted by theory. Suppose a theory on revolts says: T = B + aCd and data shows R = AB + CD. Now consider the cases hypothesized NOT to cause revolts. This is t=Ab+bc+bD. Then the intersection of these last two is tR = (Ab+bc+bD)(AB+CD). Let's multiply that out. We get
tR = AABb + ABbc + ABbD + AbCD + bCcD + bCDD
The first term, AABb, contains the product Bb, which is the empty set. So AABb = 0 and vanishes. Same with the second and third terms. The fifth term, bCcD, also vanishes, and the last term can be simplified to bCD. So the result is:
tR = AbCD + bCD
Note that bCD implies AbCD and so the longer term is redundant. This yields a final formula of:
tR = bCD
which pinpoints the shortcomings in the theory. It tells you exactly where there are peasant revolts that are not predicted by theory. Specifically, cases in which there is no commercialization, middle peasants, and absentee landlords.
Table 10 gives some real data to work with.


Copyright (c) 1997 by Stephen P. Borgatti.
Last revised:
30 March, 2005