Profit

PROFIT (PROperty FITting) is a method of testing hypotheses about the attributes that influence people's judgement of the similarities among a set of items. As discussed above, there are two basic approaches to analyzing proximities: searching for clusters and searching for dimensions. PROFIT is a way of testing hypotheses about underlying dimensions.

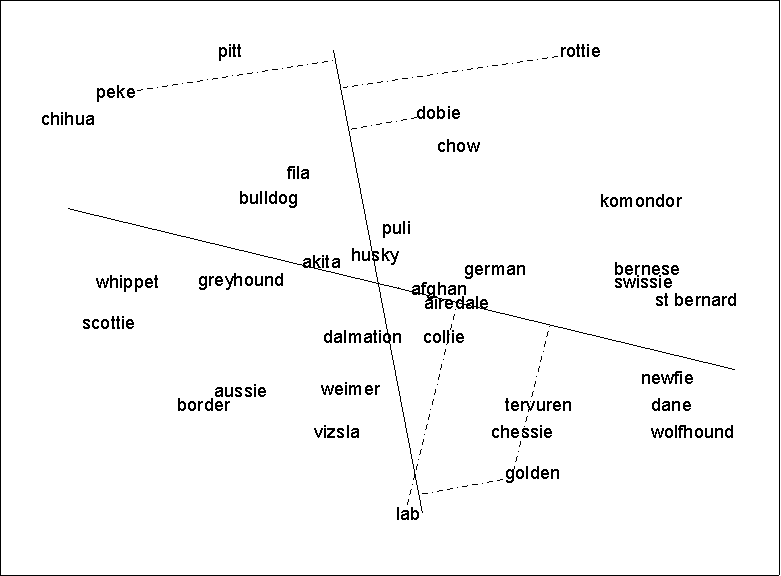
Suppose we have an MDS map, based on perceived similarities among dog breeds, such as the one shown on the next page (the data are made up). You might hypothesize that the pattern of similarities we observe is partly a function of breed size. As we move from top left to bottom right, the breeds seem to be getting larger. However, the pattern is not perfect and may in fact be more a function of my selective attention than truly present. What we need is an objective assessment of the degree to which breeds in fact get larger as we move down and right. Also, the exact direction along which breeds get larger is open to question. Perhaps it is more left-right than up-down.

The way to do this is to estimate the parameters of a model that relates breed size to position on the map, or, equivalently, relates position on the map to breed size. Putting it that way, it is apparent that what we need to do is regress breed size on map location. Map location is given by the coordinates of each breed on the map. If the map is 2-dimensional, then there are two coordinates for each breed. Hence there are two independent variables in the regression.

The dependent variable is breed size. You can get these data by looking it up in a dog book. Similarly, if you are scaling cars and you think that price is a factor in assessing similarities, then you can look up the price of each car in a reference book. However, in general this is not a good idea, because the purpose of running PROFIT is to understand the criteria that respondents used to assess similarities. To use book figures is to assume that respondents are aware of those same figures, which is unlikely. The best thing to do is to collect new data from a sample of people drawn from the same population as the respondents who generated the proximities. Have the new sample rate each item on the attribute you have hypothesized. In our case, we would ask respondents to indicate the typical size of each dog breed, either via a rating system (such as 7-point scale), or direct estimation of the number of pounds or height at the withers, or both. The data are then averaged across respondents to produce a single value for each breed.

Both the coordinate data and the attribute data (in separate files) are input to the PROFIT program. PROFIT then performs a multiple regression using the coordinates as independent variables and the attribute as the dependent variable. If you have more than one attribute, such as size, ferocity, retrieving ability, length of hair, etc., the program performs a separate regression for each one. For each attribute, there are two key outputs: an r-square statistic and the direction cosines.

The r-square tells you whether location on the map was related to values of the attribute (i.e., does size really increase as you go from left to right?). The higher the r-square, the closer the relationship. For domains with less than 20 items, the rule of thumb is that you need an r-square of at least .80 to support a conclusion that the hypothesized attribute was driving the perceived similarities among items. (And of course, you can never prove it, even with an r-square of 1.0. However, a low r-square does disprove the hypothesis.)

The direction cosines are rescalings of the regression coefficients. They give the relative contribution of each axis of the map to the prediction of the attribute. In other words, they tell you what precise direction the attribute increases along. For example, for the dog data, both cosines are positive, which means that breed size increases you move both east and north on the map. However, the cosine for the horizontal (X) axis is larger than the cosine for the vertical (Y) axis. This means that larger breeds are more east than they are north.

We use the direction cosines to draw arrows representing the attributes on the map. The values of the direction cosines give the coordinates of the head of the arrow. The middle of the arrow is always located at the dead center of the map (coordinates 0,0). To draw the arrow, draw a line from the spot indicated by the by the direction cosines (the head), through the center of the map, and out the other side. If the attribute data were coded in such a way that bigger numbers meant more of the attribute, then we draw an arrowhead at the spot indicated by the direction cosines, as shown below. Otherwise, we draw an arrowhead at the other end of the line. The arrowhead always points in the direction of increasing attribute values.

To interpret the line, do NOT think of it as a boundary separating dogs above the line from those below the line: this is totally wrong. Instead, draw perpendicular lines from each dog to the PROFIT arrow (see map on next page). This is called the projection of location onto breed size. The length of the line from the dog to the arrow is utterly irrelevant. It means absolutely nothing. What matters is where the line from the dog meets the arrow. If the line is closer to the arrowhead then another line is, then dog associated with the first line is (predicted to be) larger than the dog associated with the second line. For example, in the picture, the doberman ("dobie") is predicted to be larger than the pitbull ("pitt"). The square of the correlation between these projections and the actual breed size is equal to the r-square discussed above.

TOOLS,PROFIT

PURPOSE Evaluate the correspondence between one or more item attributes and the location of items in a multidimensional space.

DESCRIPTION PROFIT is typically used to test hypotheses regarding the attributes respondents may have used to evaluate similarities among a set of items in a cultural domain. Two sets of data are required. First, a set of coordinates for the items in a multidimensional space. Typically, these are the output of an MDS performed on pilesort or triads data. Second, a set of scores for each item on one or more attributes. Typically, these are average ratings obtained via n-point rating scales, or via paired comparisons.

Given these data, the program then performs one or more multiple regressions in which the independent variables are the map coordinates, and the dependent variable is an attribute. A separate regression is performed for each attribute. The resulting regression coefficients (suitably normalized) are used to locate the head of a vector (one for each attribute) that passes through the origin. The further an item is located away from the origin in the director of this vector, the greater the predicted value of the attribute.

PARAMETERS Map coordinates:

Name of dataset whose values represent coordinates of items (rows) in multidimensional space (the columns are dimensions).

Attributes:

Name of dataset whose values represent scores of items on one or more attributes. The dataset name should be followed by the keyword ROWS (if the attributes are rows) or COLUMNS (if the attributes are columns), followed by a list of numbers indicating which rows or columns to analyze.

(OUTPUT) Vector coordinates:

Name of dataset to contain coordinates of the original points (the items), plus coordinates of the heads of vectors representing attributes.

LOG FILE First the results of all the regressions are printed. Then an MDS map containing both items and attributes is printed.

COMMENTS Missing values are ignored. On printing the output, the first thing to do is to draw lines from the head of the arrow through the zero point, and out the other side. Convention dictates that r-squares less than .8 do not indicate support for any hypothesized attribute.

REFERENCES Kruskal, J.B. and M. Wish. n.d. Multidimensional Scaling. Beverly Hills: Sage Publications.