A Quorum of Graph Theoretic Concepts

Stephen P. Borgatti
Sociology Dept., University of South Carolina

Teacher's Corner is a regular column edited by Stephen P. Borgatti. The objective of the column is to share material helpful to the teaching of network analysis. Contributions to the column are appreciated. Contributions should be short (normally 2 pages or less), and should consist of explanations of network concepts, course syllabi, synopses of famous works, and anything else appropriate to the main objective.

One of the mathematical underpinnings of network analysis is graph theory. In this column I present a kind of glossary of what I would consider to be a minimum working vocabulary of graph-theoretic terms and notation. The reader should be aware, however, that "...uniformity in graphical terminology will never be attained, and is not necessarily desirable." (Harary 1969, p.8).

A graph (which represents an observed social relation such as "is friends with") is denoted G(V,E) and consists of a set of points V(G) together with a set of lines E(G) that connect the points. Points (which represent social actors) are also known as vertices and nodes. Lines (which represent social ties) are also known as edges, and links. Each line connects two points, which are its endpoints. The points connected by a line are said to be adjacent. In contrast, a line that has a given point as an endpoint is said to be incident upon that point. Two lines that share an endpoint are also said to be incident.

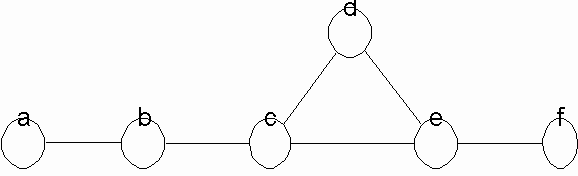
An example of a graph is given in Figure 1. It is important to note that the placing of points in the two-dimensional plane of the figure is arbitrary and conveys no information: the only meaningful property preserved by the pictorial representation is which node is linked to which other. Of course, the artist is free to locate points in accordance with some additional criteria, such as placing more central nodes towards the middle, but such a choice is no more valid than any other.

Figure 1. A graph.

Graphs may be directed or undirected. A directed graph, or digraph, is one in which the lines have direction (represented iconically with arrowheads). Directed edges are often referred to as arcs.These are used to represent potentially non-symmetric social relations, such as "is the boss of" and "likes". An undirected graph is one in which the lines do not have direction. These are used to represent logically symmetric social relations, such as "is married to" or "had sex with". Often, the term "graph" is used in contrast to "digraph" to refer specifically to undirected graphs. The underlying graph of a digraph is the graph one obtains if one removes all direction from the arcs. That is, in the underlying graph, nodes u and v are tied if and only if u-->v or u<--v.

Graphs may be reflexive or non-reflexive. In reflexive graphs, it is possible for a node to have a tie with itself, which is called a loop or, redundantly, a self-loop. In non-reflexive graphs, such links are excluded. Reflexive graphs are most commonly used to represent networks of collectivities, such as phone calls among cities.

Graphs may be valued or non-valued. A valued graph has numbers attached to the edges, which may be used to indicate the strength, capacity, frequency, duration or other quantitative measurement of the link.

The degree of a node is the number of nodes it is adjacent to; or, equivalently, it is the number of edges that are incident upon it. A node with no degree (degree 0) is an isolate. A node with degree 1 is called a pendant. The graph in Figure 1 contains two pendants and no isolates.

In a digraph, the indegree of a node is the number of arcs coming in to a node from others, while the outdegree is the number of arcs from the node to all others. More technically, the indegree of a node u is |{(x,u): (x,u)0E}|, where the vertical bar notation |S| gives the number of elements in set S. Similarly, the outdegree of u is given by |{(u,x): (u,x)0E}|. A node with positive outdegree but no indegree is called a source. A node with positive indegree but no outdegree is called a sink.

A subgraph H of a graph G is a graph whose points and lines are also in G, so that V(H) f V(G) and E(H) f E(G). If we select a set of nodes S from a graph G, and then select all the lines that connect members of S, the resulting subgraph H is called an induced subgraph of G based on S. Two points are adjacent in H if and only if they are adjacent in G.

A walk is a sequence of adjacent points, together with the lines that connect them. In other words, a walk is an alternating sequence of points and lines, beginning and ending with a point, in which each line is incident on the points immediately preceding and following it. The points and lines in a walk need not be distinct. For example, in Figure 1, the sequence a-b-c-b-c-d is a walk. A path is a walk in which no node is visited more than once. The sequence a-b-c-d is a path. A cycle is like a path except that it begins and ends with the same node (e.g. c-d-e-c).

A set of walks that share no points is called vertex-disjoint. A set of walks that share no edges is called edge-disjoint. Obviously, vertex-disjoint paths are also edge-disjoint. If a pair of nodes are connected by three vertex-disjoint paths, this means that there are three, completely independent ways of getting from one point to the other. In Figure 1, there is only one edge-disjoint path from a to f, but two edge disjoint-paths from c to d.

The length of a walk is given by the number of lines it contains. A geodesic path is a shortest path between two points. There can be more than one geodesic path joining a given pair of points. The graph-theoretic distance or geodesic distance between two points is the length of a shortest path between them. In a diffusion process, one expects faster diffusion among nodes that are close together than among nodes that are far apart.

A graph is connected if there exists a path from every node to every other. A maximal connected subgraph is called a component. A maximal subgraph is a subgraph that satisfies some specified property (such as being connected) and to which no node can be added without violating the property. For example, in Figure 1, the subgraph induced by {a,b,c} is connected, but is not a component because it is not maximal: we could add node d and the subgraph induced would still be connected. The graph in Figure 1 has just one component, which is the whole graph.

A digraph that satisfies the connectedness definition given above (i.e. there exists a path from every node to every other) is called strongly connected. That is, for any pair of nodes a and b, there exists both a path from a to b and from b to a. A digraph is unilaterally connected if between every unordered pair of nodes there is at least one path that connects them. That is, for any pair of nodes a and b (and a … b), there exists a path from either a to b or from b to a. A digraph whose underlying graph is connected is called weakly connected.

A maximal strongly connected subgraph is a strong component. A maximal weakly connected subgraph is a weak component. A maximal unilaterally connected subgraph is a unilateral component.

A cutpoint is a node whose removal would disconnect the graph. Alternatively, we could define a cutpoint as a node whose removal would increase the number of components of the graph. In the figure, nodes b, c, and e are cutpoints, while a, d, and f are not. A network that contains a cutpoint will break apart if the person who occupies the cutpoint leaves. A block is a subgraph which contains no cutpoints. A cutset is a set of points whose removal would disconnect a graph. A minimal cutset is a cutset that contains the minimum possible number of nodes that disconnect the graph. The size of a minimal cutset is called the vertex connectivity of the graph, and is denoted 6. The smaller the value of 6, the greater the vulnerability of the network to disconnection. We can also define a pairwise version of vertex connectivity, 6(u,v), which gives the minimum number of nodes that must be removed in order to disconnect vertex u from vertex v.

A bridge is a line whose removal disconnects the graph. An edge cutset is a set of lines whose removal disconnects the graph. A minimum weight cutset is an edge cutset which, for non-valued graphs, contains the fewest possible number of edges or, for valued-graphs, contains edges whose values add to the smallest possible value. The size of a minimum weight cutset is called the edge connectivity of the graph, and is denoted 8. As with point connectivity, we can also define a pairwise version of vertex connectivity, 8(u,v), which gives the minimum number of edges that must be removed in order to disconnect vertex u from vertex v.

Menger's theorem states that the minimum number of nodes that must be removed to disconnect node u from node v, (i.e. 6(u,v)) is equal to the maximum number of vertex-disjoint paths that join u and v. This also works for lines: the edge-connectivity 8(u,v) is equal to the maximum number of edge-disjoint paths that join u and v. ‘

Harary, F. 1969. Graph Theory. Reading, MA: Addison-Wesley.