notes by Steve Borgatti
1. Review of Correlation of Two Vectors
Suppose A and Y are two column vectors. Suppose they are standardized. What’s the correlation between them? Sum(AiYi)/n
In matrix or vector notation, this is 1/nA’Y. You remember that A’Y is basically correlation, right? So what is it if mean centered but not standardized? Sum(AiYi)/(n||A||*||Y||)
In textbooks, you often see A’Y defined as ||A||*||Y||Cos(theta). Theta is the angle between A and Y in geometric space. This tells you that cos(theta) is a measure of correlation, since ).
[figure 2.6 in textbook]
A’Y has another interpretation as well. It is the projection of A along the axis defined by Y.
2. Multiplying a series of row vectors (collected into a matrix ) by a vector of weights
Let the matrix be X. Let the vector of weights by V. Suppose it has just two columns and n rows. Each row is a row vector. XV is a new vector Z.
So this gives the projection of each row in X onto the dimension defined by V.
[figure 2.8 in textbook]
3. Orthogonality
Two vectors are orthogonal if they are at right angles of each other. We can express this mathematically as A’B = 0. in other words, if the correlation between them is zero. In other words, if the cos of the angle between them is 0.
[figure 2.9 in textbook]
A matrix V of many column vectors is orthogonal if V’V = I. i.e., if every pair of column vectors V1’V2 = 0. if V is standardize by columns, this means the columns are uncorrelated.
4. Rotation of Axes
Suppose X is a matrix of column vectors. And V is an orthogonal matrix. Say column 1 is .707 .707, a 45 deg ray. What vector is orthogonal to it? -707 707. test it.
[figure 2.9 again]
Suppose we multiply XV to get Z.
What is Z? first column is projection of the row points of X onto coordinate system defined by col 1 of V. 2nd col is projection of the points onto coord sys defined by col 2 of V. In other words, is a rotation of X to new coordinate system defined by V. is clockwise rotation of points 45 deg. Or counterclockwise rotation of axes by 45 deg.
Called a rigid rotation. To rotate any specified number of degrees, multiply all points by this:
Cos(theta) Sin
-Sin Cos
Here's some height by weight data:
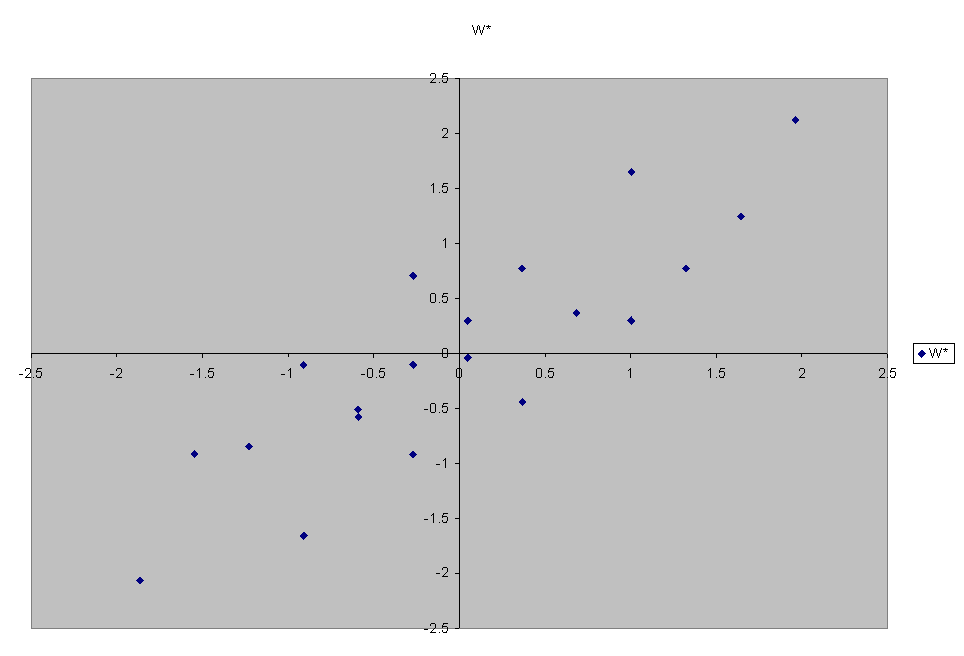
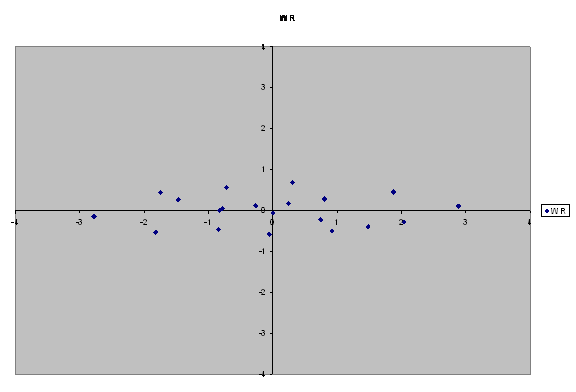
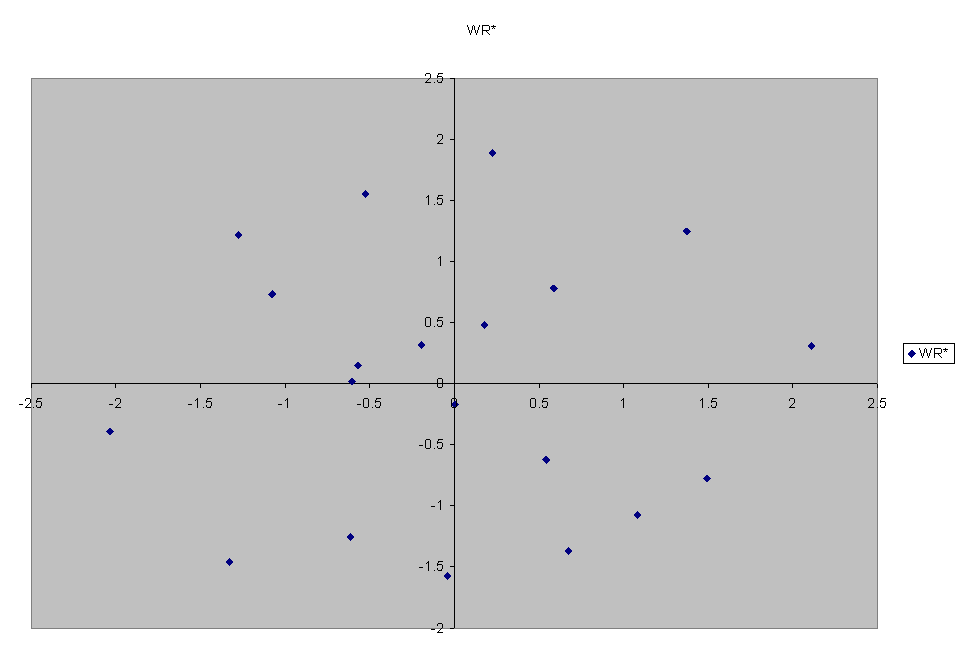
| Height | Weight | H-hbar | W-wbar | H* | W* | HR | WR | HR* | WR* |
| 57 | 93 | -6 | -31 | -1.86532 | -2.06601 | -2.77945 | -0.14189 | -2.03443 | -0.38922 |
| 58 | 110 | -5 | -14 | -1.54646 | -0.91822 | -1.74253 | 0.444163 | -1.27546 | 1.218429 |
| 60 | 99 | -3 | -25 | -0.90874 | -1.66091 | -1.81674 | -0.53178 | -1.32978 | -1.45878 |
| 59 | 111 | -4 | -13 | -1.2276 | -0.85071 | -1.46937 | 0.266464 | -1.07551 | 0.730966 |
| 61 | 115 | -2 | -9 | -0.58989 | -0.58064 | -0.82756 | 0.006536 | -0.60574 | 0.01793 |
| 60 | 122 | -3 | -2 | -0.90874 | -0.10803 | -0.71886 | 0.566108 | -0.52617 | 1.552949 |
| 62 | 110 | -1 | -14 | -0.27103 | -0.91822 | -0.8408 | -0.45757 | -0.61543 | -1.2552 |
| 61 | 116 | -2 | -8 | -0.58989 | -0.51313 | -0.77983 | 0.05427 | -0.5708 | 0.148875 |
| 62 | 122 | -1 | -2 | -0.27103 | -0.10803 | -0.26799 | 0.115243 | -0.19616 | 0.316135 |
| 63 | 128 | 0 | 4 | 0.047829 | 0.297073 | 0.243845 | 0.176215 | 0.178484 | 0.483395 |
| 62 | 134 | -1 | 10 | -0.27103 | 0.702172 | 0.304818 | 0.688053 | 0.223113 | 1.88747 |
| 64 | 117 | 1 | -7 | 0.366686 | -0.44561 | -0.0558 | -0.57429 | -0.04084 | -1.5754 |
| 63 | 123 | 0 | -1 | 0.047829 | -0.04051 | 0.005174 | -0.06246 | 0.003787 | -0.17133 |
| 65 | 129 | 2 | 5 | 0.685544 | 0.364589 | 0.742444 | -0.22692 | 0.543437 | -0.62247 |
| 64 | 135 | 1 | 11 | 0.366686 | 0.769688 | 0.803417 | 0.284922 | 0.588066 | 0.7816 |
| 66 | 128 | 3 | 4 | 1.004402 | 0.297073 | 0.920143 | -0.50008 | 0.673504 | -1.37183 |
| 67 | 135 | 4 | 11 | 1.32326 | 0.769688 | 1.479714 | -0.39138 | 1.083086 | -1.07362 |
| 66 | 148 | 3 | 24 | 1.004402 | 1.647403 | 1.874826 | 0.454601 | 1.37229 | 1.247065 |
| 68 | 142 | 5 | 18 | 1.642118 | 1.242304 | 2.039286 | -0.28267 | 1.492668 | -0.77542 |
| 69 | 155 | 6 | 31 | 1.960975 | 2.120018 | 2.885263 | 0.112443 | 2.111885 | 0.308455 |
Plot of the mean-centered data:

Now we rotate by multiplying by
.707 -.707
.707 .707
5. Stretching and Shrinking
We can stretch a picture up and down or left and right by simply multiplying each column of X by some constant > 0. If > 1 then stretch otherwise is shrink. Often expressed by storing the constants in a diagonal matrix D’ and multiplying XD-1.
For example, let D contain the std deviations of each column in X (which is mean centered). Then multiplying X by D-1 would adjust the configuration along each axis to have same length
6. SVD
Suppose we rotate and then stretch a data matrix X, to yield U. i.e. U= XVD-1
Now let’s solve for X.
UD = XV
UDV-1 = UDV’ = X
X is nxm, U is nxm, D is mxm and V is mxm as is V’.
Let’s write that differently.
Xij = SUMk( UikDkkVjk)
Xij = Ui1*D11*Vj1 + Ui2*D22*Vj2 + …
Suppose we sort columns of U , the rows and columns of D and columns of V so that the singular values are in descending order. Then we can drop off the ones in which Dkk are small. So we can approximate the matrix:
Xij == Ui1*D11*Vj1 + Ui2*D22*Vj2 + …
X is nxm, U is nxp, D is pxp and V is mxp
7. Generalized inverse
X = UDV’
X-1 = (UDV’)-1
X-1 = (V’)-1D-1U-1
X-1 = VD-1U’
\
So we can compute the inverse of any matrix via svd. Presto.
8. Principal components
Eigenvectors
9. Correspondence Analysis
Step 1. normalization of the data. Square root transformation.
Hij = fij/sqrt(fi.)*sqrt(f.j)
Step 2. svd of normalized matrix H = UDV’
Step 3. rescale the Us and Vs. this part varies.
Xik = Uik/sqrt(f../fi.)
Yjk = Vjk/sqrt(f../f.j)
Fij = fi.f.j/f..(1 + sumk(dk*xik*yjk)
Chisq/n = Sum(dk) for k > 1 (exclude trivial first factor).