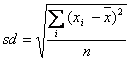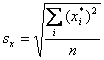Notes on Vectors

Definition

an ordered list of values
a 1-dimensional array
usually conceived of as columns, but can be rows as well
a vector v has elements v_i where 0 < i <= n
n is the number of values, also known as the order of a vector
each number v_i is a "value"

Context

Vectors are ubiquitous in research, modeling, math
Have numerous alternative interpretations, including geometric ones
set of coordinates in space
Variables (columns in a data matrix)
Cases (rows in a data matrix)

Simple Linear Combinations

a scalar is a number -- i.e., not a vector or matrix. A constant.
u = 5+v means create a new vector u whose ith value u_i = 5 + v_i
in other words, we add 5 to every value of vector v
same with subtraction, multiplication, division.
a simple linear combination is mx+b, where we multiple each value in x by the constant m and then add b (be sure to do multiplication and division before addition/subtraction)
a linear combination of the form mx+b is a linear transformation or a rescaling of a vector. In many contexts, a linear rescaling is considered trivial -- it is a transformation that doesn't change the vector in an essential way. E.g., can express a temperature in Fahrenheit or Centigrade or Kelvin
F = (9/5)C + 32
C = (F-32)(5/9) = 5/9F - 32*5/9

Aggregations

Sums, Means, Magnitudes

Sum of all values in vector v is:

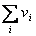
Average is the sum divided by n, the number of elements in the vector. can write it as
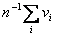
In many situations, the average and the sum are interchangeable, since the average is just a rescaling of the sum.
The average is a special case of the mean. The mean is a weighted average. When the weights are all equal and sum to 1, the mean is the average.
The average is often used to summarize with just one value a set of numbers. Finding the center of a distribution (when the distribution is unimodal, as in a normal distribution)
Can also interpret the average as giving the typical magnitude of the values in a vector. But this only works if all the values are non-negative (otherwise the positives and negatives cancel)
Having calculated the mean of a vector, you can mean-center the vector by subtracting the mean from each value in the vector, creating a new vector, often denoted with an asterisk. E.g.,

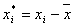
the Euclidean norm (aka L2 norm, aka the length of a vector) is the square root of the sum of squares of the elements of a vector

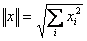
If a vector represents the coordinates of a point in euclidean space, the norm gives the distance from the center of the space

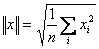
Advantage over the mean is that it works nicely with a mix of positive and negative numbers

Dispersion

standard deviation is calculated as

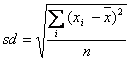
the SD is typical deviation of each value in a vector from the mean of the vector.
This is actually the true or population SD. Sometimes we divide by n-1 when calculating from a sample and trying to estimate the population SD
Another way to calculate it that makes this clear is by mean-centering the vector (obtaining x*) and then computing RMS of the meancentered variable:

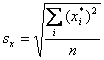
the mean is the value that is least different from all values in the vector, when you define least difference as the sum of squared differences. The implication is that there is no value that you could replace x-bar with that would yield a smaller standard deviation.
The standard deviation of a vector x+b, where b is constant, is the same as the std dev of the the original vector x
the standard deviation of a vector mx where m is a constant, is just m times the std dev of the original vector

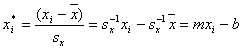
Dot products and Outer Products

The dot product of X and Y, or X×Y (or even simply XY), refers to multiplying x_i by y_i for each i and summing up the products. The result is a single value.

X = [1 1 2 2]

Y = [1 2 3 4]

X×Y = 1*1 + 1*2 +2*3 +2*4

One way to think of it is as the the weighted sum of the elements of Y, where the weights are given by X.

The outer product of two vectors is more complex and the result is a matrix. Consequently, we discuss this in more detail in a later lecture. For now, however, we just show that the outer product of X and Y is the following matrix:

1	1	2	2
2	2	4	4
3	3	6	6
4	4	8	8