Role

1. Structural equivalence as a formalization for the notion of role

a. requires parents to have same children, and all doctors to have same patients.
b. you and i play the same role as customers of a bank, but we shouldn't be required to have the same tellers.
c. every parent must be connected to all children to be seen as playing the same role
d. can't be used across components

2. SE as structural similarity

a. SE should be a basis for structural studies that posit that structurally similar nodes should have similar outcomes
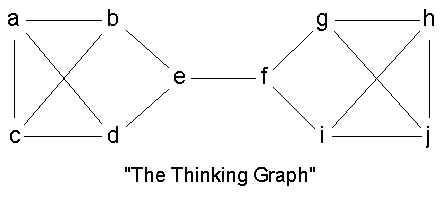
b. but SE misses similarities in structure. See thinking graph. a and j are structurally identical, but since they don't have any links in common, are not SE

3. SE and cohesion

• would like to be alternative to cohesion, but actually, SE nodes are never more than 2 links apart. In large network with paths of length 50 or more, clusters of nodes that are 2 links apart look more like cohesive subgroups than structural classes
• confounds similarity with proximity

4. Regular Equivalence

a. for all these reasons, regular equivalence was invented by White and Reitz (83)
b. definition 1 (relations approach):

if a = b then

(i) for all c s.t. aRc, there exists d such that d = c and bRd,
(ii) for all c s.t. cRa, there exists d such that d = c and dRb

c. definition 2 (colorations approach):

if c(a) = (b) then c(n(a)) = c(n(b))

d. definition 3 (image graphs):

c(n(a)) = c(n(b)) <--> n(c(a)) = n(c(b))

e. definition 4 (blockmodels):

if a matrix block contains a one, then every row and column in the block must contain at least one one.

5. Interpretation

a. social roles

• cuts across components
• whereas nodes are SE if connected to the same others, if they are RE they are connected to equivalent others,
• captures relational role notion: what society or organization is is a set of roles, like vp finance, research project director, foreman, etc, which have a characteristic set of relations with other roles

b. note that SE nodes are RE as well. RE is a broader view of structural similarity.

• if SE finds nodes that occupy same position, RE finds nodes that occupy similar positions, or finds positions that are similar
  

6. The lattice of regular equivalences

a. most graphs have more than one regular equivalence/coloring
b. structural equivlaence is a regular equivalence
c. the set of all regular equivalences forms a lattice
i. a lattice is a relation that forms a quasi-order, and which has an element that "includes" all the rest and another element that is included by all the rest.
ii. in the RE lattice, the infimum is the coloring in which every node has its own color
iii. the supremum varies in directed graphs, but in undirected is always the complete partition
(1) when analyzing directed graphs, we always want the maximal RE
(2) when analyzing undirected graphs, we never want the maximal RE

7. Automorphic equivalence

a. one member of the RE lattice that is above SE but below maximum element is automorphic equivalence.
b. a permutation is a 1-to-1 mapping of the nodes of a graph to the nodes of the graph, so that (v) yields some node. Can write permutations two ways:
i. mapping notation:

ii. cycle notation: (a d e) (g h j i)
iii. the identity permutation is the one that maps every node to itself
c. an automorphism is a permutation of nodes such that (a,b) E iff ( (a) = (b).
i. in terms of adjacency matrix, A = (A)
ii. in thinking graph, the set of all automorphisms is

1: 1 2 3 4 5 6 7 8 9 10
2: 1 2 3 4 5 6 7 10 9 8
3: 1 2 3 4 5 6 9 8 7 10
4: 1 2 3 4 5 6 9 10 7 8
5: 1 4 3 2 5 6 7 8 9 10
6: 1 4 3 2 5 6 7 10 9 8
7: 1 4 3 2 5 6 9 8 7 10
8: 1 4 3 2 5 6 9 10 7 8
9: 3 2 1 4 5 6 7 8 9 10
10: 3 2 1 4 5 6 7 10 9 8
11: 3 2 1 4 5 6 9 8 7 10
12: 3 2 1 4 5 6 9 10 7 8
13: 3 4 1 2 5 6 7 8 9 10
14: 3 4 1 2 5 6 7 10 9 8
15: 3 4 1 2 5 6 9 8 7 10
16: 3 4 1 2 5 6 9 10 7 8
17: 8 7 10 9 6 5 2 1 4 3
18: 10 7 8 9 6 5 2 1 4 3
19: 8 9 10 7 6 5 2 1 4 3
20: 10 9 8 7 6 5 2 1 4 3
21: 8 7 10 9 6 5 4 1 2 3
22: 10 7 8 9 6 5 4 1 2 3
23: 8 9 10 7 6 5 4 1 2 3
24: 10 9 8 7 6 5 4 1 2 3
25: 8 7 10 9 6 5 2 3 4 1
26: 10 7 8 9 6 5 2 3 4 1
27: 8 9 10 7 6 5 2 3 4 1
28: 10 9 8 7 6 5 2 3 4 1
29: 8 7 10 9 6 5 4 3 2 1
30: 10 7 8 9 6 5 4 3 2 1
31: 8 9 10 7 6 5 4 3 2 1
32: 10 9 8 7 6 5 4 3 2 1
d. an equivalence is automorphic if for all a,b in V, a = b iff there exists in Aut(G) such that (a) = b.
i. orbit equivalence is the maximal automorphic equivalence]
ii. in thinking graph, its {a,c,h,j} {b,g,d,i} {e,f}

8. Differences between equivalences

a. unlike RE in general, OE demands that equivalent n odes be connected to the same number of nodes of different types, so a parent with 1 kid is different from a parent with 3.
i. in general this may mean that OE is not as useful for modelling the general role concept as is the MAXRE.
b. but OE is a purely structural version of structural equivalence
i. SE has problem that if a,b have same outcome, don't know if its for structural reasons, or because they are connected to same maddening individuals
ii. SE also permanently confounds and is limited by proximity: must be within 2 nodes at all times.
(1) most structural processes do not have this proximity thing built in to them: think of power in exchange network.
(2)