Cohesive Subgroups

 

Overview

Two basic reasons why we are interested in defining and detecting subgroups in network data. The theoretical is to provide a structural definition of the sociological notion of group. The practical is to obtain data reduction/description of patterns of observed dyadic cohesion.

We assume that groups will be more homogeneous with respect to key variables than other subgraphs either because of either homophily or diffusion.

 

Data Reduction Approach

a. find dense regions of the network
b. cluster analysis of adjacency matrix (particularly if you have valued data.)
c. cluster analysis of other cohesion index, such as geodesic distance, maximum flow

 

Theoretical approach

Several formal definitions of subgroups have been advanced. I review a few:

1. clique (Luce & Perry 1949):

  1. a maximally complete subgraph
  2. note that density of clique is perfect 1: everyone connected to all others all possible ties present
  3. also, distance from everyone to everyone is minimal: 1.
  4. overlapping
  5. can be numerous
  6. too stringent in some cases, but depends on the relation studied
  7. Some relaxations developed, along two different lines
    1. based on distances within group (n-clique, n-clan, n-club)
    2. based on density/number of ties present (k-plex)

2. n-clique (Luce 1950):

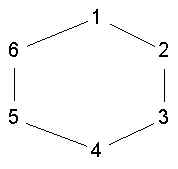
  1. a maximal set of nodes such that all pairs of nodes in the set are distance n or less
  2. but one problem with nclique is that even a 2-clique is not very cohesive. In the graph {1,3,5} is a 2-clique, but none are connected to each other.
  3. also, from substantive point of view is wierd that shortest path between two members requires outside intermediary

3. n-clan: (Alba 19xx) an nclique such that the induced subgraph has diameter n or less

4. n-club: (Mokken 19xx) a maximal subgraph of diameter <= n

  1. every n-clan is an n-club and every n-clan is an n-clique
  2. but every n-club is not an n-clan or n-clique, although it is contained in them (fail n-clique maximality condition)
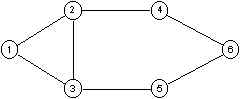  • 2-cliques: {1,2,3,4,5}, {2,3,4,5,6};
  • 2-clan {2,3,4,5,6};
  • 2-clubs {1,2,3,4}, {1,2,3,5} and {2,3,4,5,6}

 

5. k-plex (Seidman 19xx):

  1. a (maximal) subgraph in which each member is connected to at least n-k other members.
  2. when k = 1 each person is connected to all other members = clique.
  3. 2-plexes are quite cohesive, at least if we observe some basic rules:
  4. if you remove a node from a kplex, the residual subgraph is still a kplex (if we ignore maximality rule)
  5. kplexes with k < (n+2)/2 vertices cannot contain bridges (but may contain cutpoint)

6. ls-sets (Seidman):

  1. Let alpha(K) be the number of ties from members of a set K to non-members. Let alpha(X,Y) be the number of ties from members of X to members of Y. A subset H of V is an LS -set iff for any proper subset K of H, alpha(K) > alpha(H)
  2. or, H is ls iff alpha(K,H-K) > alpha(K,V-H)
  3. 1,2,3,4 is ls

 

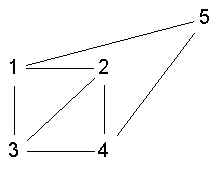
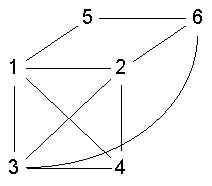
  1. 1,2,3,4 is not ls

 

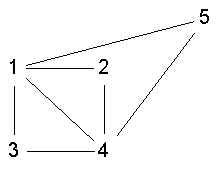
  1. 1,2,3,4 is a clque but not ls

 

7. lambda sets

i. one property of ls sets is that each nodes in the set has more edge indep paths to each other node in the set than to nodes outside the set.
ii. lambda sets have that definition
iii. same as clustering max flow matrix.

Cohesive Regions

A related concept is that of a cohesive region. A cohesion region is an area within which there are subgroups.

1. Component

  1. A maximal set of nodes which are mutually reachable.

2. k-cores (seidman):

  1. Let delta(H) represent the minimum number of ties that any node in H has to the other nodes in H. A K-Core is a maximal subgraph in which delta(H) >= k.
  2. a graph is a tree iff no 2-cores
  3. connected graph has just one 2-core
  4. any k-core contains at least k+1 vertices
  5. vertices in different k-cores cannot be adjacent
  6. all kplexes are contained with kcores.
  7. a 1-core is just a component.

 

Home Borgatti Analytic Technologies INSNA Connections